Podstawy trapezu prostokątnego mają długości \(6\) i \(10\) oraz tangens jego kąta ostrego jest równy \(3\). Oblicz pole tego trapezu.
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Oznaczmy sobie wszystkie długości, które są podane w treści zadania oraz oznaczmy kąt ostry, którego znamy wartość tangensa:
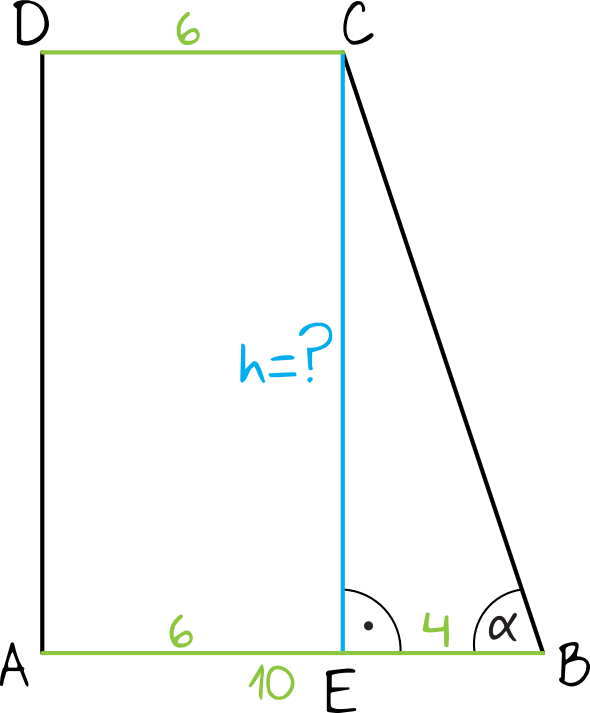
Od razu też zaznaczyliśmy sobie, że skoro \(|AE|=|DC|\), to \(|EB|=10-6=4\).
Krok 2. Wyznaczenie długości wysokości trapezu, czyli odcinka \(CE\).
Wykorzystamy tutaj wartość tangensa (który jest równy \(3\)) oraz obliczoną przed chwilą długość odcinka \(EB\):
$$tgα=\frac{|CE|}{|EB|} \\
3=\frac{|CE|}{4} \\
|CE|=12$$
Wysokość trójkąta jest więc równa \(h=12\).
Krok 3. Obliczenie pola trapezu.
Znamy długości obydwu podstaw, obliczyliśmy przed chwilą wysokość trapezu, tak więc możemy wszystkie te dane podstawić do wzoru na pole trapezu:
$$P=\frac{1}{2}(a+b)\cdot h \\
P=\frac{1}{2}(6+10)\cdot12 \\
P=\frac{1}{2}\cdot16\cdot12 \\
P=96$$
Odpowiedź:
\(P=96\)


Jaka by była odpowiedź gdyby Tanges kąta ostrego był równy 1,5?
Wystarczyłoby wtedy w drugim kroku zamiast 3 podstawić 1,5 ;) Odcinek CE byłby wtedy dwa razy krótszy, czyli i pole byłoby dwa razy mniejsze.
jak obliczyć w nim obwód?
Długość boku AD będzie taka sama jak CE. Brakującą długość BC policzylibyśmy z Twierdzenia Pitagorasa (trójkąt EBC jest prostokątny i wiemy, że dolna przyprostokątna ma długość 4, a boczna ma 12) :)