Podstawa trójkąta równoramiennego ma długość \(6\), a ramię ma długość \(5\). Wysokość opuszczona na podstawę ma długość:
\(3\)
\(4\)
\(\sqrt{34}\)
\(\sqrt{61}\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
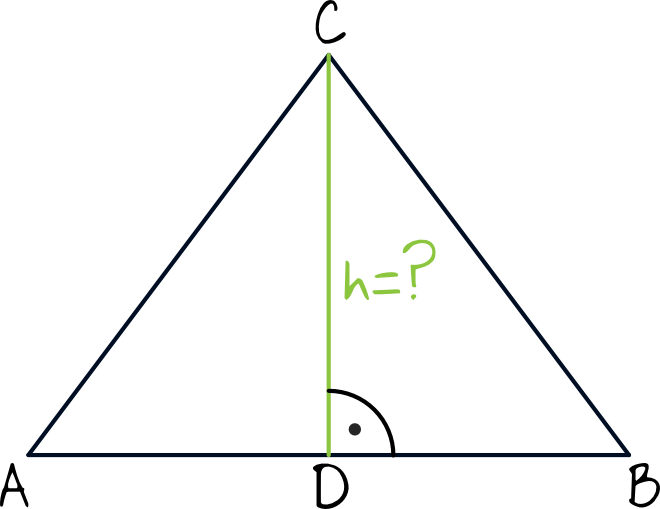
Z rysunku wynika kluczowa informacja – wysokość trójkąta (która jest jednocześnie przyprostokątną trójkąta \(BDC\)) da się wyznaczyć z Twierdzenia Pitagorasa.
Krok 2. Obliczenie wysokości trójkąta.
Skorzystamy tutaj z Twierdzenia Pitagorasa.
$$a^2+b^2=c^2 \\
3^2+b^2=5^2 \\
9+b^2=25 \\
b^2=25-9 \\
b^2=16 \\
b=4 \quad\lor\quad b=-4$$
Wartość ujemną odrzucamy, bo wysokość trójkąta musi mieć wartość dodatnią.
Wysokość trójkąta jest więc równa \(4\).
Odpowiedź:
B. \(4\)

