Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Z treści zadania wiemy, że w podstawie ostrosłupa mamy kwadrat (oznaczmy sobie jego bok jako \(a\)). Wiemy też, że ściany boczne są trójkątami równobocznymi. Możemy więc powiedzieć, że w takim razie wszystkie krawędzie tej bryły mają jednakową miarę i jest ona równa \(a\). Dodatkowo możemy dostrzec, że skoro w podstawie jest kwadrat, to przekątna \(AC\) będzie mieć długość \(a\sqrt{2}\). Całość więc będzie wyglądać następująco:
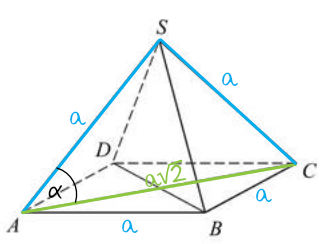
Krok 2. Dostrzeżenie połowy kwadratu i wyznaczenie miary kąta \(SAC\).
Na powyższym rysunku zaznaczyliśmy sobie trójkąt \(ASC\). Ma on ramiona o długości \(a\) i podstawę o długości \(a\sqrt{2}\). W tym momencie powinniśmy dostrzec, że to jest tak naprawdę połówka kwadratu o boku \(a\). Taka obserwacja prowadzi nas do wniosku, że kąt \(ASC\) jest kątem prostym, a kąty \(SAC\) oraz \(ACS\) mają po \(45°\). Nas interesuje właśnie miara kąta \(SAC\), zatem prawidłową odpowiedzią jest wartość \(45°\).