Podstawą ostrosłupa ABCD jest trójkąt ABC. Krawędź AD jest wysokością ostrosłupa

Podstawą ostrosłupa \(ABCD\) jest trójkąt \(ABC\). Krawędź \(AD\) jest wysokością ostrosłupa (zobacz rysunek).

Oblicz objętość ostrosłupa \(ABCD\), jeżeli wiadomo, że \(|AD|=12\), \(|BC|=6\), \(|BD|=|CD|=13\).

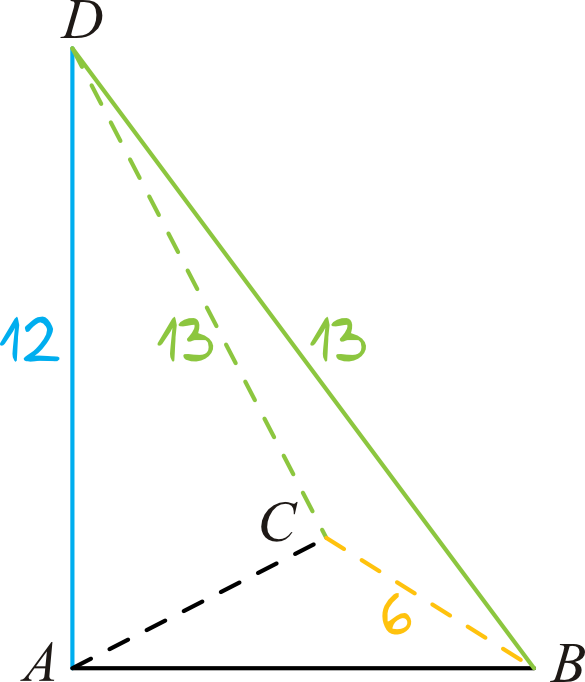
W zasadzie do obliczenia objętości brakuje nam tylko pola podstawy, bo wysokość bryły już znamy. Aby obliczyć to pole to potrzebna byłaby wysokość trójkąta, który znalazł się w podstawie. Wyliczymy ją bez problemu jeśli poznamy długości boków \(AB\) i \(AC\) i właśnie od tego rozpoczniemy obliczenia.

Skorzystamy tutaj z Twierdzenia Pitagorasa. Aby obliczyć bok \(AB\) wystarczy wziąć do obliczeń duży trójkąt \(ABD\), którego miary dwóch boków są nam znane, a więc:
$$a^2+b^2=c^2 \\
|AB|^2+|AD|^2=|BD|^2 \\
|AB|^2+12^2=13^2 \\
|AB|^2+144=169 \\
|AB|^2=25 \\
|AB|=5 \quad\lor\quad |AB|=-5$$

(wartość ujemną odrzucamy, bo bok nie może mieć długości ujemnej)

Długość boku \(AC\) wyliczymy dokładnie w ten sam sposób, tyle tylko że skorzystamy z trójkąta \(ACD\). Jego wymiary są identyczne co trójkąta \(ABD\) (są to więc trójkąty przystające), a więc i bok \(AC\) ma długość \(5\).

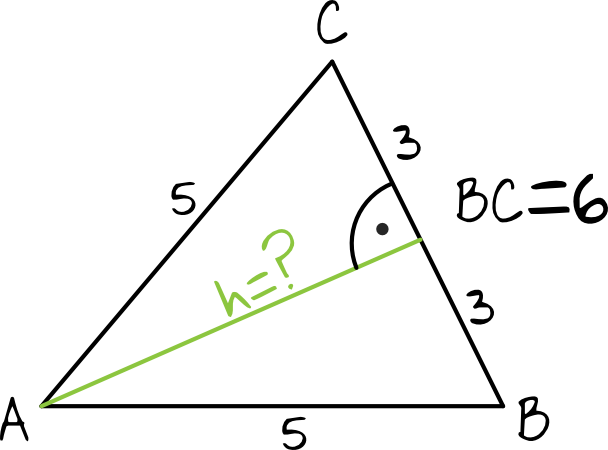
W podstawie mamy trójkąt równoramienny, a więc jego wysokość podzieli nam bok \(BC\) na dwie równe części. Wysokość trójkąta wyliczymy więc używając ponownie Twierdzenia Pitagorasa.
$$a^2+b^2=c^2 \\
h^2+|CE|^2=|AC|^2 \\
h^2+3^2=5^2 \\
h^2+9=25 \\
h^2=16 \\
h=4 \quad\lor\quad h=-4$$

(wartość ujemną oczywiście odrzucamy)

$$P_{p}=\frac{1}{2}a\cdot h \\
P_{p}=\frac{1}{2}\cdot6\cdot4 \\
P_{p}=12$$

Znając już wszystkie potrzebne miary możemy bez problemu obliczyć objętość ostrosłupa:
$$P_{p}=12 \\
H=12 \\
V=\frac{1}{3}\cdot P_{p}\cdot H \\
V=\frac{1}{3}\cdot12\cdot12=48$$

Objętość ostrosłupa jest równa \(48\).