Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanieśmy na rysunek dane z treści zadania i wprowadźmy też proste oznaczenia kluczowych długości:
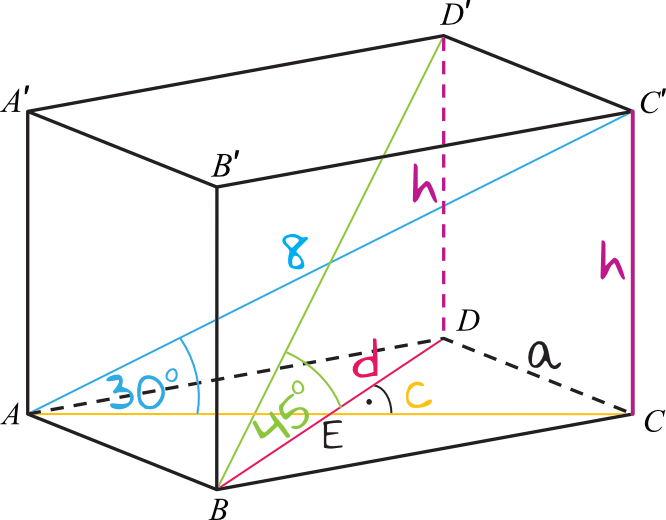
Skoro w podstawie graniastosłupa znajduje się romb to warto pamiętać, że przekątne rombu mają różne długości oraz przecinają się w połowie swojej długości pod kątem prostym. Dzięki tym własnościom rombu będziemy w stanie wyliczać poszczególne długości.
Krok 2. Wyznaczenie długości pierwszej przekątnej podstawy.
Spójrzmy na trójkąt prostokątny \(ACC'\). Odcinek \(AC\) oznaczony na rysunku jako \(c\) jest przekątną podstawy, którą wyliczymy korzystając z funkcji trygonometrycznych.
$$cos30°=\frac{c}{8} \\
\frac{\sqrt{3}}{2}=\frac{c}{8} \\
c=\frac{8\sqrt{3}}{2} \\
c=4\sqrt{3}$$
Krok 3. Obliczenie wysokości graniastosłupa.
Nadal patrzymy na trójkąt prostokątny \(ACC'\). Znamy już dwie długości w tym trójkącie, więc trzecią długość, czyli wysokość \(CC'\) oznaczoną jako \(h\) możemy policzyć zarówno z Twierdzenia Pitagorasa jak i funkcji trygonometrycznych. Korzystając tym razem z sinusa zapiszemy, że:
$$sin30°=\frac{h}{8} \\
\frac{1}{2}=\frac{h}{8} \\
h=4$$
Krok 4. Wyznaczenie długości drugiej przekątnej podstawy.
Teraz spójrzmy na trójkąt \(BDD'\). Zawiera się w nim długość drugiej z przekątnych rombu, czyli bok \(BD\) oznaczony symbolem \(d\). Ten trójkąt jest nie tylko trójkątem prostokątnym, ale także jest to trójkąt równoramienny (bo jest to trójkąt o kątach \(45°, 45°, 90°\)). W związku z tym przyprostokątne tego trójkąta mają tą samą długość, a to z kolei oznacza, że:
$$d=h=4$$
Krok 5. Obliczenie pola podstawy graniastosłupa.
Znając długości przekątnych rombu możemy obliczyć pole podstawy, a będzie ono równe:
$$P_{p}=\frac{1}{2}\cdot c\cdot d \\
P_{p}=\frac{1}{2}\cdot4\sqrt{3}\cdot4 \\
P_{p}=2\sqrt{3}\cdot4 \\
P_{p}=8\sqrt{3}$$
Krok 6. Wyznaczenie długości boku rombu.
Spójrzmy na trójkąt \(CDE\). Jest to trójkąt prostokątny, bo przekątne rombu przecinają się pod kątem prostym. Wiemy też, że przekątne przecinają się w połowie swojej długości, zatem:
$$|CE|=\frac{1}{2}\cdot c \\
|CE|=\frac{1}{2}\cdot4\sqrt{3} \\
|CE|=2\sqrt{3} \\
\quad \\
|DE|=\frac{1}{2}d \\
|DE|=\frac{1}{2}\cdot4 \\
|DE|=2$$
Skoro tak, to odcinek \(DC\), oznaczony symbolem \(a\), który jest długością boku rombu wyliczymy z Twierdzenia Pitagorasa:
$$|CE|^2+|DE|^2=a^2 \\
(2\sqrt{3})^2+2^2=a^2 \\
4\cdot3+4=a^2 \\
12+4=a^2 \\
a^2=16 \\
a=4 \quad\lor\quad a=-4$$
Ujemne rozwiązanie oczywiście odrzucamy, bo długość nie może być ujemna, zatem zostaje nam \(a=4\).
Krok 7. Obliczenie pola powierzchni całkowitej graniastosłupa.
Mamy już wszystkie potrzebne dane do obliczenia pola powierzchni całkowitej graniastosłupa. W skład tej powierzchni wejdą dwa pola podstawy (góra i dół) obliczone w piątym kroku (\(P_{p}=8\sqrt{3}\)) oraz cztery ściany boczne o wymiarach \(4\times4\). Zatem:
$$P_{c}=2P_{p}+4P_{b} \\
P_{c}=2\cdot8\sqrt{3}+4\cdot4\cdot4 \\
P_{c}=16\sqrt{3}+64$$