Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Przekątna podstawy, wysokość graniastosłupa oraz przekątna bryły tworzą taki oto trójkąt prostokątny:
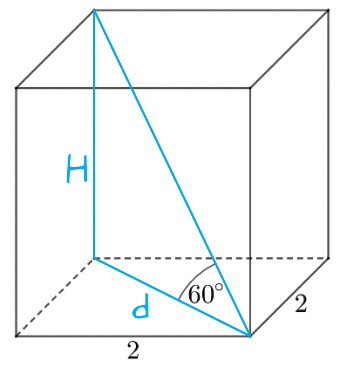
Krok 2. Obliczenie długości przekątnej podstawy.
W podstawie mamy kwadrat o boku długości \(2\). Z własności kwadratów wynika, że kwadrat o boku \(a\) będzie miał przekątną o długości \(a\sqrt{2}\), zatem:
$$d=2\sqrt{2}$$
Krok 3. Obliczenie wysokości graniastosłupa.
Spoglądamy na zaznaczony na rysunku trójkąt prostokątny. Korzystając z tangensa możemy zapisać, że:
$$tg60°=\frac{H}{2\sqrt{2}} \\
\sqrt{3}=\frac{H}{2\sqrt{2}} \\
H=\sqrt{3}\cdot2\sqrt{2} \\
H=2\sqrt{6}$$