Rozwiązanie
To zadanie rozwiążemy sobie na dwa sposoby:
I sposób - obliczając obwody trójkąta i trapezu.
Krok 1. Obliczenie długości boku \(BC\).
Korzystając z Twierdzenia Pitagorasa możemy obliczyć, że:
$$12^2+16^2=|BC|^2 \\
144+256=|BC|^2 \\
|BC|^2=400 \\
|BC|=20$$
Krok 2. Obliczenie obwodu trójkąta \(ABC\).
Trójkąt \(ABC\) ma obwód równy:
$$Obw_{ABC}=16cm+12cm+20cm=48cm$$
Krok 3. Obliczenie długości przecięcia.
Wiemy, że bok \(AC\) został podzielony przerywaną linią na dwie równe części, zatem powstała nam taka oto sytuacja:
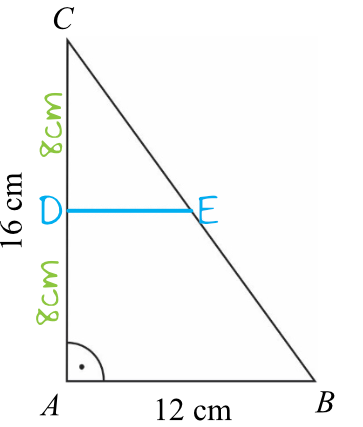
Trójkąt \(DEC\) jest trójkątem podobnym do \(ABC\) (mają jednakowe miary kątów). Skoro tak, to stosunek długości odpowiadających boków musi być jednakowy, zatem możemy ułożyć następującą proporcję:
$$\frac{|AB|}{|DE|}=\frac{|AC|}{|DC|} \\
\frac{12}{|DE|}=\frac{16}{8}$$
Mnożąc na krzyż otrzymujemy:
$$16\cdot |DE|=96 \\
|DE|=6$$
Krok 4. Obliczenie długości ramion trapezu.
Spróbujmy nanieść na nasz trapez te wszystkie długości, które już znamy:
Kluczowe miary tego trapezu wyglądają następująco:
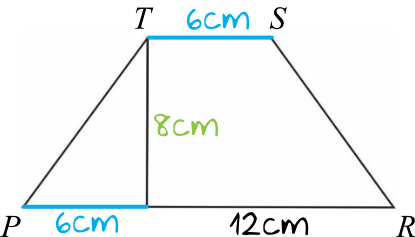
Do obliczenia obwodu trapezu brakuje nam jeszcze znajomości długości odcinków \(PT\) oraz \(SR\), czyli ramion trapezu. Te dwa odcinki są na pewno równej długości, bowiem jest to trapez równoramienny. Z Twierdzenia Pitagorasa jesteśmy w stanie wyliczyć długość ramienia \(PT\):
$$6^2+8^2=|PT|^2 \\
64+36=|PT|^2 \\
|PT|^2=100 \\
|PT|=10$$
Wyszło nam więc, że ramiona tego trapezu mają długość \(10cm\).
Krok 5. Obliczenie obwodu trapezu \(PRST\).
Znamy już wszystkie miary w trapezie, zatem dodając do siebie poszczególne długości otrzymamy obwód równy:
$$Obw_{PRST}=6cm+12cm+10cm+6cm+10cm=44cm$$
Krok 6. Obliczenie różnicy obwodów.
Skoro obwód trójkąta jest równy \(48cm\), a obwód trapezu to \(44cm\), to różnica obwodów wynosi:
$$48cm-44cm=4cm$$
II sposób - bez liczenia dokładnych wartości obwodów trójkąta i trapezu.
Moglibyśmy rozwiązanie tego zadania nieco uprościć, bowiem tak prawdę mówiąc to nie ma konieczności obliczania długości ramion trapezu, a tym samym nie ma konieczności obliczania dokładnych obwodów obydwu figur. Z rysunku wynika, że miara odcinka \(CB\) jest równa sumie długości ramion \(PT\) oraz \(SR\). Naszym zadaniem jest podanie jedynie różnicy między obwodem trójkąta i trapezu, więc skoro te odcinki są sobie równe to możemy je pominąć. W związku z tym wystarczyłoby dojść do trzeciego kroku z pierwszego sposobu rozwiązania i porównać sumę odcinków \(|AB|+|AC|\) z sumą \(|PR|+|TS|\). Skoro tak, to:
$$|AB|+|AC|=12cm+16cm=28cm \\
|PR|+|TS|=6cm+12cm+6cm=24cm$$
To oznacza, że różnica obwodów wynosi:
$$28cm-24cm=4cm$$