Ostrosłup prawidłowy to ostrosłup, który w swojej podstawie ma figurę foremną i którego wysokość pada na środek tej podstawy. Gdyby ktoś nie pamiętał to przypomnę, że figura foremna to taka, która ma wszystkie boki i kąty jednakowej miary.
To jaka figura znajduje się w podstawie ostrosłupa ma też wpływ na pełną nazwę bryły. Przykładowo:
• ostrosłup prawidłowy trójkątny ma w swojej podstawie trójkąt równoboczny
• ostrosłup prawidłowy czworokątny ma w swojej podstawie kwadrat
• ostrosłup prawidłowy pięciokątny ma w swojej podstawie pięciokąt foremny
Najbardziej charakterystycznym ostrosłupem prawidłowym jest czworościan foremny, którego wszystkie ściany są trójkątami równobocznymi. Można więc powiedzieć, że czworościan jest szczególnym przypadkiem ostrosłupa prawidłowego trójkątnego.
Własności ostrosłupa prawidłowego
Bardzo podobnie jak ma to miejsce w przypadku graniastosłupów prawidłowych, tak i tutaj będziemy często spotykać się z ostrosłupami prawidłowymi ze względu na ich specjalne własności, które wynikają z własności poszczególnych figur foremnych:
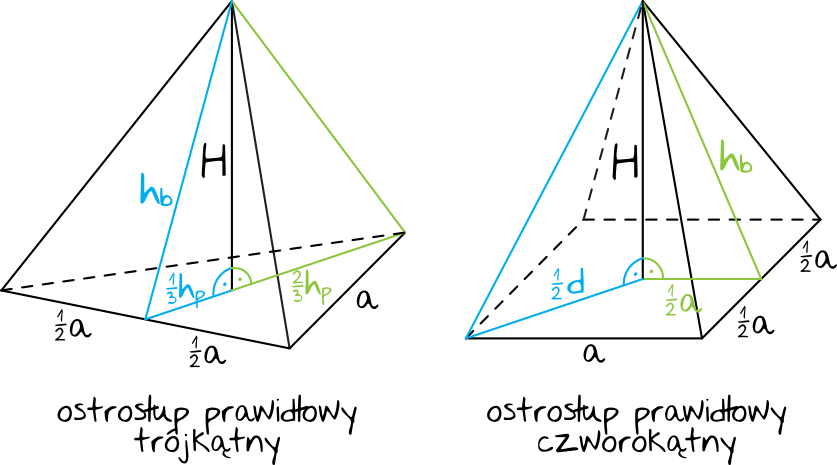
Na podstawie powyższych rysunków powiedzmy sobie o najważniejszych własnościach z których będziemy korzystać podczas rozwiązywania zadań:
Ostrosłup prawidłowy trójkątny:
• w podstawie mamy trójkąt równoboczny, zatem będziemy mogli tutaj korzystać ze wzorów \(h=\frac{a\sqrt{3}}{2}\) oraz \(P=\frac{a^2\sqrt{3}}{4}\).
• ściany boczne są zawsze trójkątami równoramiennymi – to niezwykle ważna cecha, bo dzięki niej wiemy, że wysokość ściany bocznej dzieli nam podstawę na dwie równe części.
• wysokość bryły pada na środek trójkąta równobocznego znajdującego się w podstawie. Z własności trójkątów równobocznych wiemy, że ten charakterystyczny punkt dzieli wysokość trójkąta na odcinki o długości \(\frac{1}{3}h\) oraz \(\frac{2}{3}h\) (patrz rysunek).
• powstaje nam tutaj kilka trójkątów prostokątnych (z przyprostokątną będącą wysokością całej bryły), dzięki którym będziemy mogli wyliczać różne długości boków, korzystając z Twierdzenia Pitagorasa lub funkcji trygonometrycznych.
Ostrosłup prawidłowy czworokątny:
• w podstawie mamy kwadrat, a z własności kwadratów wynika, że kwadrat o boku \(a\) ma długość \(d=a\sqrt{2}\).
• ściany boczne są trójkątami równoramiennymi (podobnie jak w ostrosłupie prawidłowym trójkątnym).
• podobnie jak w ostrosłupie prawidłowym trójkątnym powstaje nam kilka różnych trójkątów prostokątnych, które pozwolą nam wyznaczać długości boków przy użyciu Twierdzenia Pitagorasa lub funkcji trygonometrycznych.
