Rozwiązanie
Oś symetrii zawsze przechodzi przez wierzchołek paraboli:
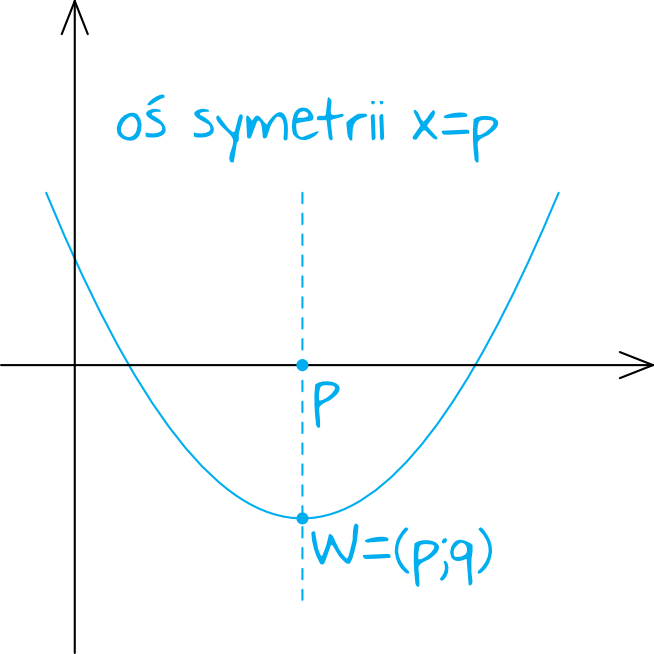
Widzimy więc, że musimy poznać współrzędną \(p\) wierzchołka naszej paraboli, a w tym celu możemy posłużyć się następującym wzorem:
$$p=\frac{-b}{2a}$$
Współczynniki \(b\) oraz \(a\) odczytamy wprost ze wzoru funkcji \(f(x)=\frac{1}{3}x^2+4x+7\). Funkcja ta jest zapisana w postaci ogólnej \(f(x)=ax^2+bx+c\), zatem widzimy, że w naszym przypadku \(a=\frac{1}{3}\) oraz \(b=4\). Podstawiając te współczynniki do wzoru na współrzędną \(p\), otrzymamy:
$$p=\frac{-4}{2\cdot\frac{1}{3}} \\
p=\frac{-4}{\frac{2}{3}} \\
p=(-4)\cdot\frac{3}{2} \\
p=-6$$
To oznacza, że osią symetrii będzie prosta o równaniu \(x=-6\).