Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro promień dużego okręgu jest równy \(2\), to otrzymamy następującą sytuację:
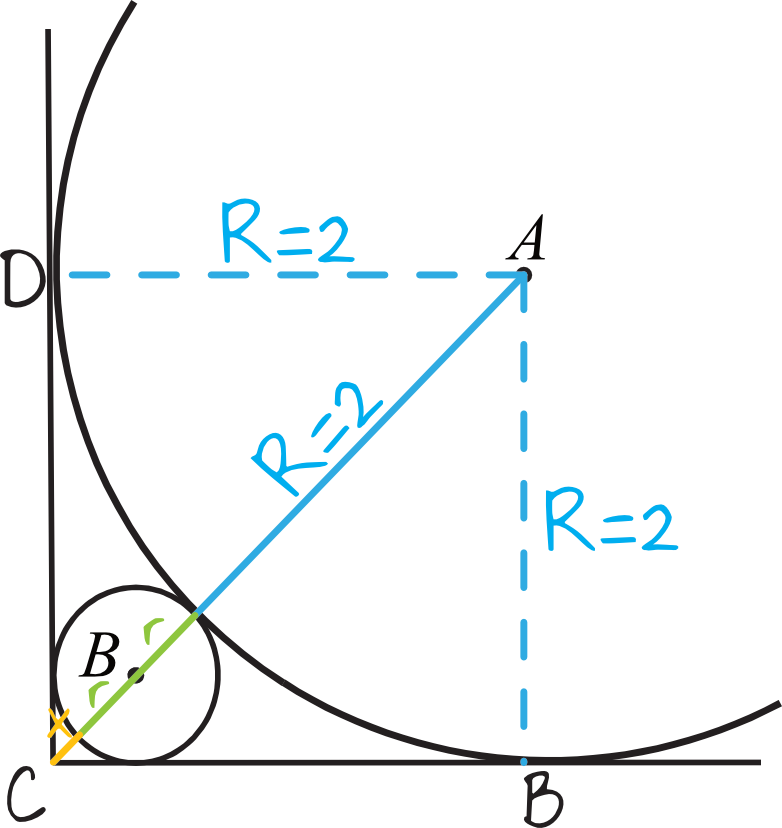
Krok 2. Ułożenie równania.
Na rysunku powstał nam kwadrat \(ABCD\), którego boki są równe długości promienia okręgu. Z własności przekątnych kwadratu wiemy, że kwadrat o boku \(a\) ma przekątną równą \(a\sqrt{2}\). Nasz kwadrat \(ABCD\) ma bok długości \(2\), a skoro tak, to odcinek \(AC\) będący przekątną tego kwadratu ma długość \(2\sqrt{2}\). To oznacza, że możemy zapisać iż:
$$x+r+r+2=2\sqrt{2} \\
x+2r+2=2\sqrt{2}$$
Krok 3. Analiza otrzymanego równania i zakończenie dowodzenia.
Wiemy, że \(x+2r+2=2\sqrt{2}\). Skoro \(x\) jest jakąś konkretną długością, to znaczy że odcinek \(2r+2\) jest mniejszy niż \(2\sqrt{2}\). W związku z tym:
$$2r+2\lt2\sqrt{2} \quad\bigg/:2 \\
r+1\lt\sqrt{2} \\
r\lt\sqrt{2}-1$$