Okrąg opisany na kwadracie ma promień \(4\). Długość boku kwadratu jest równa:
\(4\sqrt{2}\)
\(2\sqrt{2}\)
\(8\)
\(4\)
Rozwiązanie:
Krok 1. Stworzenie rysunku pomocniczego.
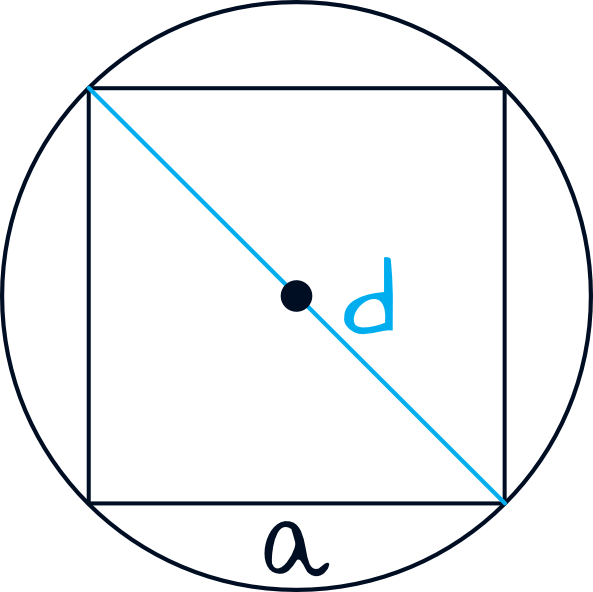
Spójrzmy na rysunek poglądowy. Widzimy wyraźnie, że średnica okręgu jest jednocześnie przekątną naszego kwadratu. Korzystając z tej wiedzy bez problemu wyliczymy długość boku kwadratu.
Krok 2. Obliczenie średnicy okręgu.
W treści zadania mamy podaną długość promienia. To największa pułapka w tym zadaniu. My musimy znać średnicę, a ta będzie równa oczywiście:
$$2\cdot4=8$$
Krok 3. Obliczenie długości boku kwadratu.
Kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). Długość przekątnej kwadratu jest równa średnicy okręgu, a więc możemy ułożyć równanie:
$$a\sqrt{2}=8 \quad\bigg/:\sqrt{2} \\
a=\frac{8}{\sqrt{2}}$$
Krok 4. Usunięcie niewymierności z mianownika:
$$a=\frac{8\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
a=\frac{8\sqrt{2}}{2} \\
a=4\sqrt{2}$$
Odpowiedź:
A. \(4\sqrt{2}\)


Długość promienia nie jest pułapką.
Długość boku kwadratu obliczymy korzystając z wzoru Pitagorasa.
Długość boku kwadratu jest przeciwprostokątną a promienie okręgu do jego sąsiednich wierzchołków są przyprostokątnymi.
Ojj nawet nie zdajesz sobie sprawy z tego jak promień/średnica może być sporą pułapką :D To o czym mówisz też jest jak najbardziej fajnym pomysłem na rozwiązanie zadania, choć chyba mniej intuicyjnym dla większości uczniów ;)