Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
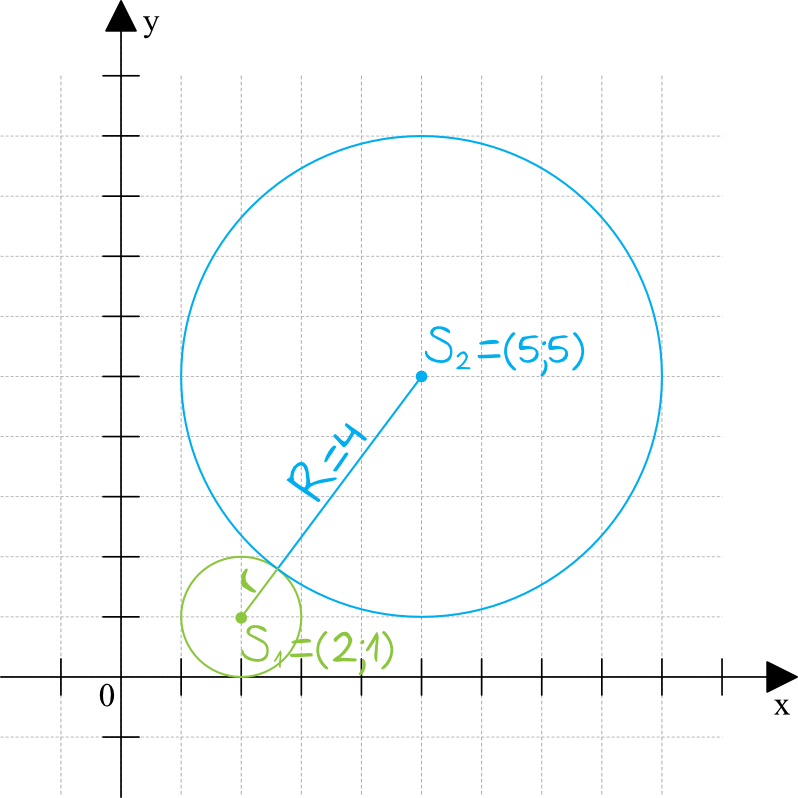
Krok 2. Obliczenie długości między środkami okręgów.
Znamy współrzędne obydwu punktów. Korzystając ze wzoru na długość odcinka w układzie współrzędnych możemy zatem zapisać, że:
$$|S_{1}S_{2}|=\sqrt{(x_{S_{2}}-x_{S_{1}})^2+(y_{S_{2}}-y_{S_{1}})^2} \\
|S_{1}S_{2}|=\sqrt{(5-2)^2+(5-1)^2} \\
|S_{1}S_{2}|=\sqrt{3^2+4^2} \\
|S_{1}S_{2}|=\sqrt{9+16} \\
|S_{1}S_{2}|=\sqrt{25} \\
|S_{1}S_{2}|=5$$
Krok 3. Obliczenie długości promienia małego okręgu.
Z rysunku widzimy, że odcinek \(S_{1}S_{2}\) jest sumą długości promieni małego i dużego okręgu. Skoro promień dużego okręgu ma miarę \(R=4\), to:
$$|S_{1}S_{2}|=r+R \\
5=r+R \\
5=r+4 \\
r=1$$