Odcinki \(AB\) i \(DE\) są równoległe. Długości odcinków \(CD\), \(DE\) i \(AB\) są odpowiednio równe \(1\), \(3\) i \(9\).
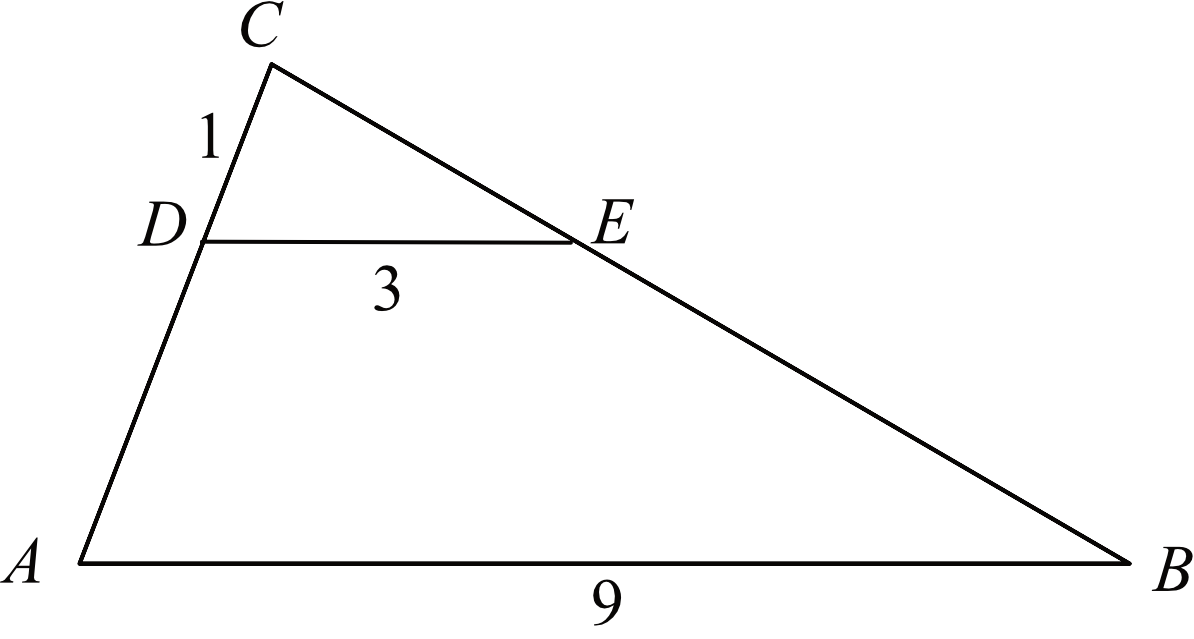
Długość odcinka \(AD\) jest równa:
\(2\)
\(3\)
\(5\)
\(6\)
Rozwiązanie:
Skorzystamy tutaj z podobieństwa trójkątów \(CDE\) oraz \(CAB\).
Krok 1. Ułożenie odpowiedniej proporcji długości boków i wyznaczenie długości odcinka \(CA\).
$$\frac{|CD|}{|DE|}=\frac{|CA|}{|AB|} \\
\frac{1}{3}=\frac{|CA|}{9}$$
Widzimy, że zgodnie z tą proporcją długość boku \(|CA|\) jest równa \(3\). Gdybyśmy tego nie dostrzegli, to można wykonać mnożenie na krzyż:
$$1\cdot9=|CA|\cdot3 \\
3\cdot|CA|=9 \\
|CA|=3$$
Krok 2. Obliczenie długości odcinka \(AD\).
Korzystając z rysunku widzimy, że:
$$|AD|=|CA|-1 \\
|AD|=3-1 \\
|AD|=2$$
Odpowiedź:
A. \(2\)

