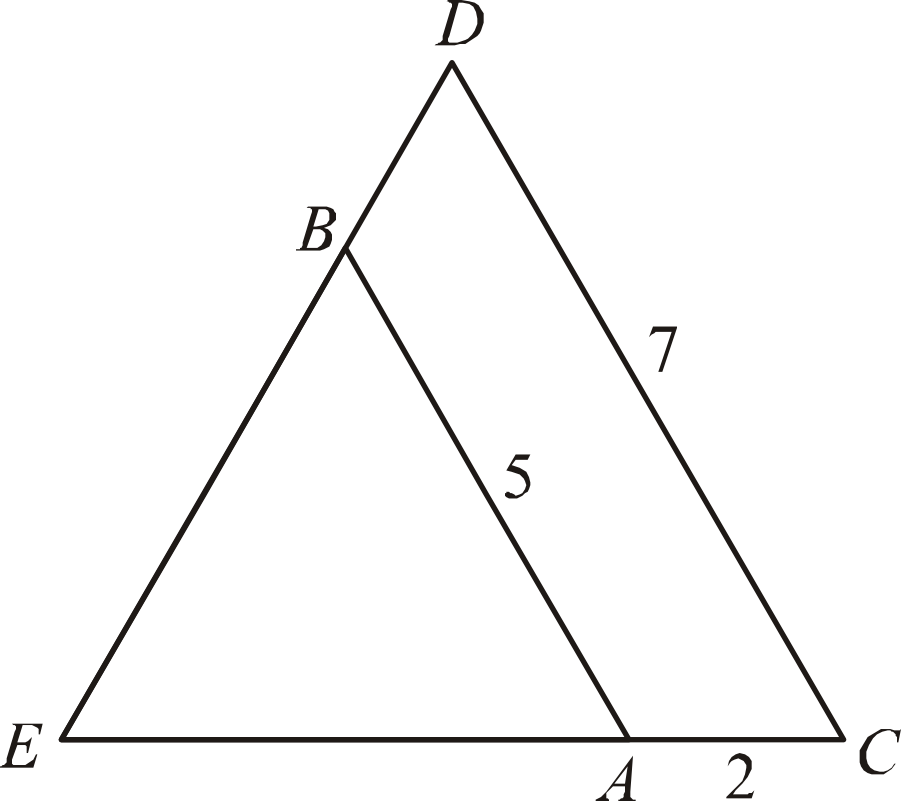
Odcinki \(AB\) i \(CD\) są równoległe i \(|AB|=5, |AC|=2, |CD|=7\) (zobacz rysunek). Długość odcinka \(AE\) jest równa:
\(\frac{10}{7}\)
\(\frac{14}{5}\)
\(3\)
\(5\)
Rozwiązanie:
Krok 1. Ułożenie odpowiedniego równania.
Skoro odcinki \(AB\) i \(CD\) są równoległe to wiemy, że trójkąty \(EAB\) i \(ECB\) są podobne. W związku z tym stosunek długości odcinka \(EC\) względem \(DC\) jest taki sam jak stosunek odcinka \(EA\) i \(BA\). Zauważmy też, że \(|EC|=|AC|+2\). Wykorzystamy tę wiedzę i ułożymy następujące równanie:
$$\frac{|EC|}{7}=\frac{|EA|}{5} \\
\frac{|EA|+2}{7}=\frac{|EA|}{5}$$
Krok 2. Rozwiązanie powstałego równania.
Równanie to możemy rozwiązać na wiele sposobów, ale najprościej jest chyba wykonać mnożenie na krzyż, zatem:
$$5\cdot(|EA|+2)=7|EA| \\
5|EA|+10=7|EA| \\
10=2|EA| \\
|EA|=5$$
Odpowiedź:
D. \(5\)

