Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Odcinki \(OC\) oraz \(BC\) są na pewno sobie równe, a to dlatego że mają długość promienia okręgu. Skoro więc z założeń zapisanych w treści zadania wynika, że odcinek \(BC\) jest równy odcinkowi \(OB\), to znaczy że trójkąt \(OBC\) jest równoboczny:
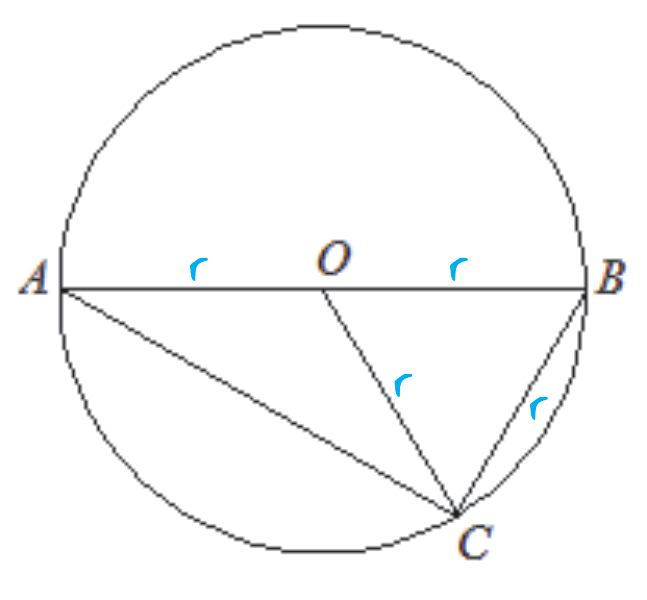
Krok 2. Obliczenie miary kąta \(AOC\).
Skoro trójkąt \(OBC\) jest równoboczny, to znaczy że wszystkie jego kąty mają miarę \(60°\). Jeden z kątów tego trójkąta (a dokładniej kąt \(COB\)) jest kątem przyległym do kąta \(AOC\). Skoro suma kątów przyległych jest równa \(60°\), to oznacza, że:
$$|\sphericalangle AOC|=180°-60°=120°$$
Krok 3. Obliczenie wartości \(sin120°\).
Do obliczenia pola powierzchni trójkąta \(AOC\) będziemy chcieli skorzystać ze wzoru na pole trójkąta:
$$P=\frac{1}{2}ab\cdot sinα$$
W związku z tym za chwilę będziemy potrzebować wartości \(sin120°\), a tej nie ma zapisanej w tablicach matematycznych. Musimy więc skorzystać ze wzorów redukcyjnych np.:
$$sin(90°+α)=cosα \\
sin120°=sin(90°+30°)=cos30°=\frac{\sqrt{3}}{2}$$
Krok 4. Obliczenie pola trójkąta \(AOC\).
Teraz możemy skorzystać ze wzoru na pole trójkąta z sinusem. W naszym przypadku \(a=r\) oraz \(b=r\), zatem:
$$P=\frac{1}{2}ab\cdot sinα \\
P=\frac{1}{2}\cdot r\cdot r\cdot sin120° \\
P=\frac{1}{2}\cdot r\cdot r\cdot\frac{\sqrt{3}}{2} \\
P=\frac{\sqrt{3}}{4}r^2$$