W tym temacie poznamy sposób na obliczenie objętości wszystkich graniastosłupów prostych i dowiemy się skąd się wzięły odpowiednie wzory.
Co to jest graniastosłup prosty?
Graniastosłupem prostym jest bryła, której ściany boczne są prostokątami. Dodatkowo wszystkie te ściany boczne muszą być prostopadłe do podstawy. Przykładem takiego graniastosłupa prostego jest prostopadłościan lub sześcian, czyli bryły które prawdopodobnie znasz już bardzo dobrze. Oprócz tych dwóch brył jest jeszcze jednak bardzo wiele innych graniastosłupów prostych, którymi się dzisiaj będziemy zajmować. Przykładowo gdyby jakiś graniastosłup miał w podstawie trójkąt, to wtedy byłby to graniastosłup prosty trójkątny. Gdyby graniastosłup miał w podstawie pięciokąt, to nazwalibyśmy tę bryłę graniastosłupem prostym pięciokątnym itd. Zanim jednak poznamy wszystkie wzory na obliczenie objętości graniastosłupów prostych to spójrzmy na prosty przykład ze znanym nam już prostopadłościanem:
Dla przypomnienia, wzór na objętość prostopadłościanu to: \(V=a\cdot b\cdot c\)
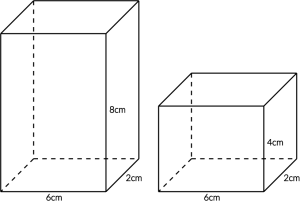
Odpowiedź: Tak! A oto dowód:
$$V_{1}=6cm\cdot2cm\cdot4cm=12cm^2\cdot4cm=48cm^3 \\
V_{2}=6cm\cdot2cm\cdot8cm=12cm^2\cdot8cm=96cm^3$$
\(96cm^3\) jest dwa razy większe od \(48cm^3\).
Powyższa prawidłowość zaszłaby także wtedy, gdybyśmy w podstawie prostopadłościanu mieli także inne wymiary długości i szerokości. Dzieje się tak, ponieważ obydwa prostopadłościany mają dokładnie to samo pole podstawy (\(6cm\cdot2cm=12cm^2\)). I to będzie właśnie nasz punkt wyjściowy do obliczeń objętości graniastosłupów prostych.
$$V=Pp\cdot H$$
gdzie:
\(V\) – objętość graniastosłupa
\(Pp\) – pole podstawy graniastosłupa
\(H\) – wysokość graniastosłupa
W tym momencie jesteśmy w stanie obliczyć objętość graniastosłupa, który w swojej podstawie ma nie tylko prostokąt, ale także trójkąt, romb, równoległobok, trapez lub jakąkolwiek inną figurę. Spójrzmy na prosty przykład:
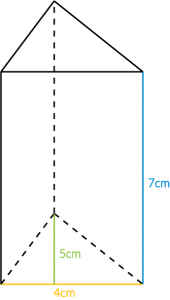
Musimy obliczyć objętość powyższego graniastosłupa, który w podstawie ma trójkąt. Obliczamy więc pole trójkąta (czyli nasze \(Pp\)), a potem całość mnożymy przez wysokość graniastosłupa (czyli przez \(H\)).
UWAGA: Nie pomyl wysokości trójkąta z wysokością graniastosłupa! To dwa zupełnie różne wymiary i nie można ich stosować zamiennie! Na naszym rysunku wysokość trójkąta ma kolor zielony, a wysokość graniastosłupa oznaczona jest na niebiesko.
$$Pp=\frac{1}{2}a\cdot h=\frac{1}{2}\cdot4cm\cdot5cm=2cm\cdot5cm=10cm^2$$
Wysokość graniastosłupa jest równa \(H=7cm\). To oznacza, że objętość naszej bryły jest równa:
$$V=Pp\cdot H=10cm^2\cdot7cm=70cm^3$$
Oczywiście, tak jak to miało miejsce w przypadku obliczania pól powierzchni, tak i wzorów na objętość możemy używać do wyznaczenia długości niektórych wymiarów naszego graniastosłupa. Spójrzmy na poniższe zadanie:
Krok 1. Znamy na pewno pole powierzchni podstawy (\(Pp\)), więc je od razu policzmy:
$$Pp=8cm\cdot2cm=16cm^2$$
Krok 2. Spróbujmy teraz podstawić do wzoru na objętość wszystkie informacje jakie uzyskaliśmy:
$$V=Pp\cdot H \\
48cm^3=16cm^2\cdot H$$
Krok 3. Szukamy wartości \(H\), która jest naszą jedyną niewiadomą we wzorze. Musimy więc odpowiedzieć sobie na pytanie jaką liczbę należy pomnożyć przez \(16\), aby uzyskać \(48\)? Tą liczbą oczywiście będzie \(3\), bo \(48:16=3\). To znaczy, że szukana wysokość ma miarę: \(H=3cm\).
Tematy i ćwiczenia z tematu brył polecane dla Ciebie:

Przydatne :-)
Przydatne :) dzięki temu się dużo nauczyłem :D
Dziękuję wam :D
Mega przydatne dziękuję
Szkoda, że nie ma objętości sześcianu
O objętości sześcianu możesz poczytać tutaj:
https://szaloneliczby.pl/objetosc-prostopadloscianu-i-szescianu/