Rozwiązanie
Krok 1. Określenie współrzędnych wierzchołka paraboli.
Funkcja kwadratowa przedstawiona jest w postaci kanonicznej, czyli takiej z której w prosty sposób możemy odczytać wierzchołek paraboli. Postać kanoniczną opisujemy jako \(y=a(x-p)^2+q\), gdzie \(p\) oraz \(q\) są współrzędnymi wierzchołka paraboli \(W=(p;q)\). Skoro znamy wzór naszej funkcji i jest ona przedstawiona dokładnie w takiej postaci jakiej potrzebujemy (nawet znaki plus i minus się zgadzają), to bez problemu odczytamy z niej współrzędne wierzchołka paraboli: \(W=(4;5)\).
Krok 2. Ustalenie najmniejszej wartości funkcji kwadratowej.
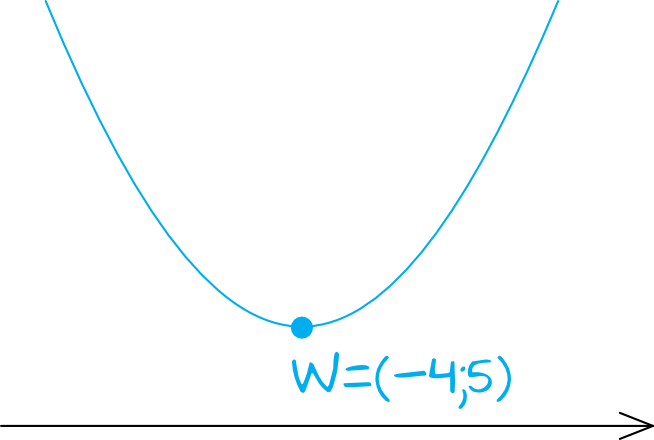
Nasza funkcja kwadratowa jest parabolą, która ma ramiona skierowane do góry (wiemy to, bo gdybyśmy przekształcili ją do postaci ogólnej, czyli wymnożyli to wszystko przez siebie, to przed \(x^2\) stałaby dodatnia wartość). Skoro tak, to najmniejszą wartość funkcja ta przyjmuje w swoim wierzchołku i my współrzędne tego wierzchołka już znamy. W związku z tym możemy stwierdzić, że nasza funkcja przyjmuje najmniejszą wartość dla argumentu \(x=-4\), a tą wartością będzie \(y=5\).