Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Aby dobrze zrozumieć istotę tego zadania to narysujmy sobie taki prowizoryczny okrąg z zaznaczonym trójkątem:
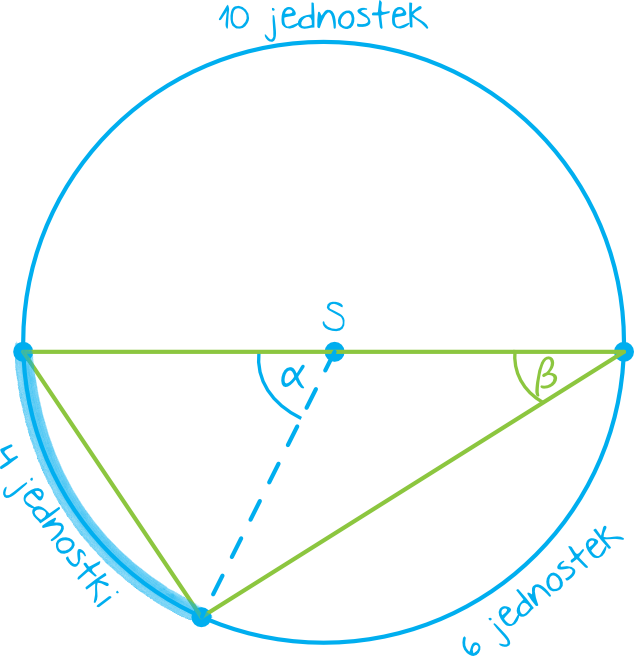
Najmniejszym kątem w tym trójkącie jest zaznaczony na zielono kąt \(β\). Tutaj kluczem do rozwiązania zadania jest dostrzeżenie, że ten kąt opiera się na tym samym łuku co kąt środkowy \(α\), którego miarę jesteśmy w stanie obliczyć.
Krok 2. Obliczenie miary kąta środkowego \(α\).
Z powyższego rysunku wynika, że cały łuk ma długość \(10+6+4=20\) jednostek. Najmniejszy kąt środkowy jest oparty na \(4\) jednostkach z \(20\), zatem jego miara będzie równa \(\frac{4}{20}\) kąta pełnego, czyli:
$$α=\frac{4}{20}\cdot360°=72°$$
Krok 3. Obliczenie miary kąta wpisanego β.
Z własności kątów środkowych i wpisanych, które są oparte na tym samym łuku wiemy, że miara kąta wpisanego będzie dwukrotnie mniejsza od miary kąta środkowego, zatem:
$$β=72°:2 \\
β=36°$$
Krok 4. Podanie przybliżonej wartości cosinusa kąta \(β\).
Zgodnie z treścią zadania musimy jeszcze podać przybliżoną wartość cosinusa naszego kąta \(β\). Z tablic możemy odczytać, że:
$$cos36°\approx0,8090\approx0,81$$