Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej \(f\). Wierzchołkiem tej paraboli jest punkt \(W=(1,9)\). Liczby \(-2\) i \(4\) to miejsca zerowe funkcji \(f\).
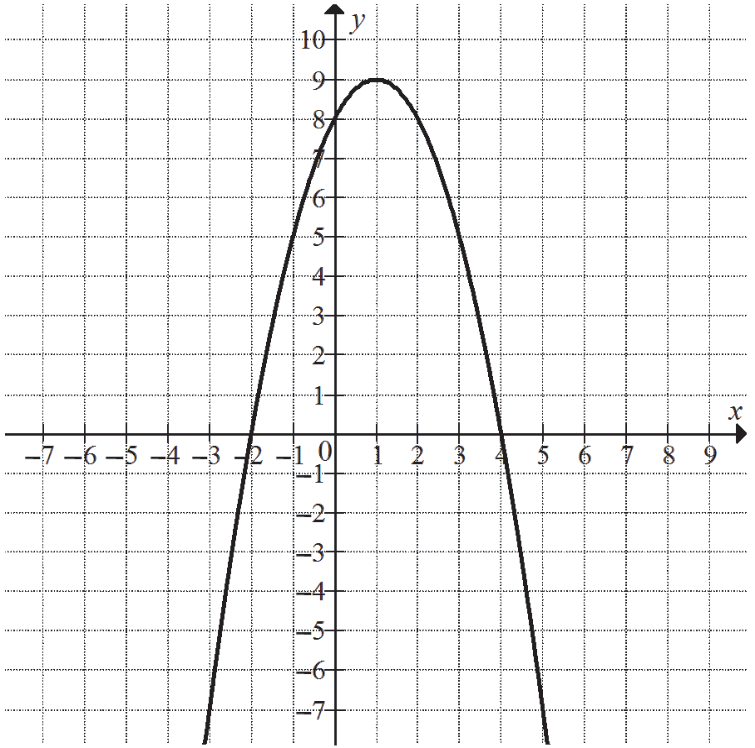
Najmniejsza wartość funkcji \(f\) w przedziale \(\langle-1,2\rangle\) jest równa:
\(2\)
\(5\)
\(8\)
\(9\)
Rozwiązanie:
Analizując wykres widzimy, że funkcja ta przyjmuje najmniejszą wartość równą \(5\) dla \(x=-1\).
Odpowiedź:
B. \(5\)

