Na rysunku przedstawiono wykres funkcji \(f\).
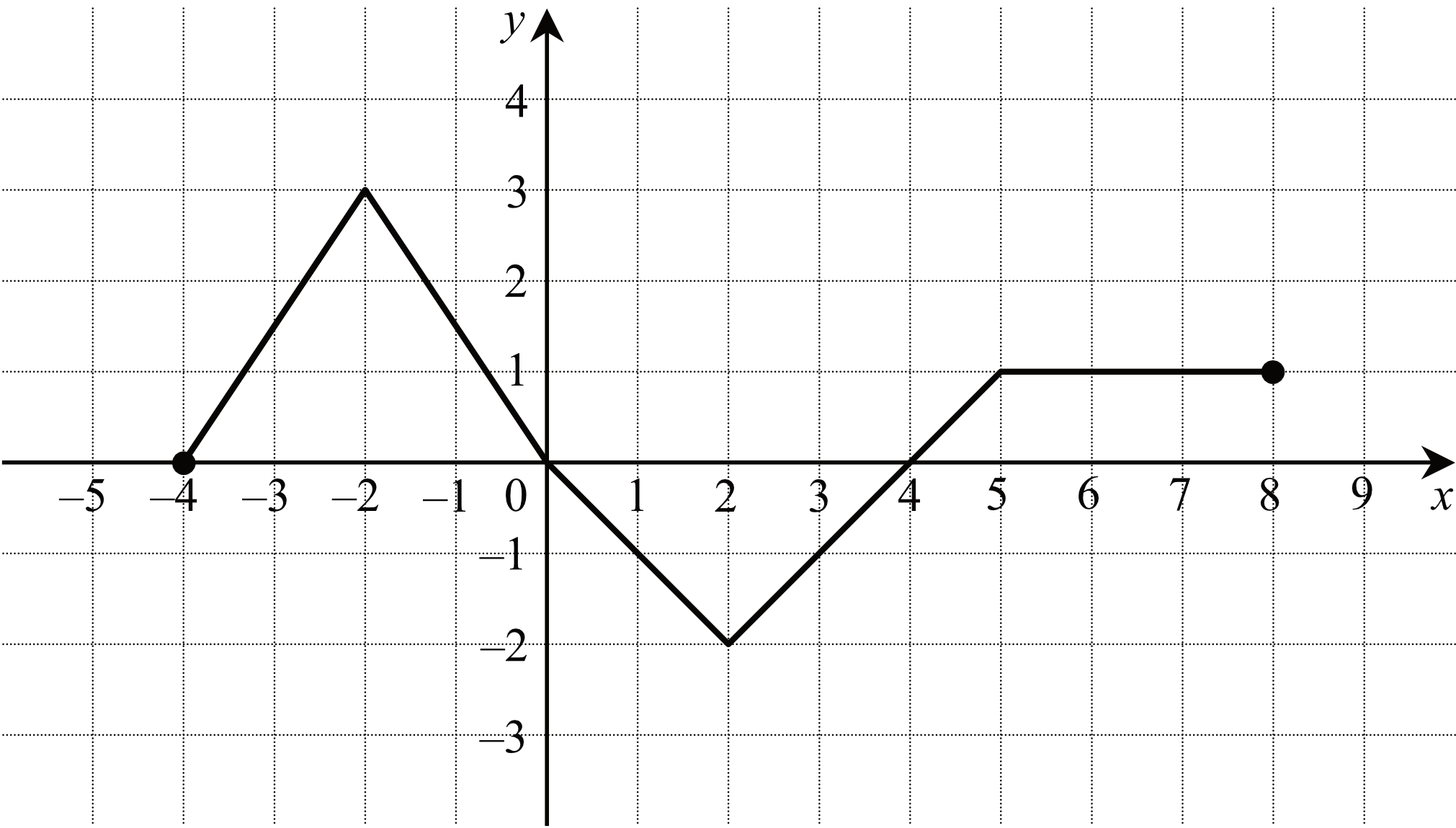
Odczytaj z wykresu i zapisz:
a) zbiór wartości funkcji \(f\),
b) przedział maksymalnej długości, w którym funkcja \(f\) jest malejąca.
Rozwiązanie:
Krok 1. Ustalenie zbioru wartości funkcji \(f\).
Odczytujemy jakie wartości na osi igreków przyjmuje nasza funkcja i widzimy wyraźnie, że wszystkie wartości funkcji mieszczą się w przedziale \(\langle-2;3\rangle\).
Krok 2. Ustalenie miejsc w których funkcja \(f\) jest malejąca.
Teraz szukamy na osi iksów takich argumentów, dla których ta funkcja jest malejąca. Jest tylko jeden taki przedział (więc siłą rzeczy będzie on maksymalnej długości), a tym przedziałem jest \(\langle-2;2\rangle\).
Odpowiedź:
a) \(\langle-2;3\rangle\)
b) \(\langle-2;2\rangle\)

