Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanieśmy na rysunek następujące informacje:
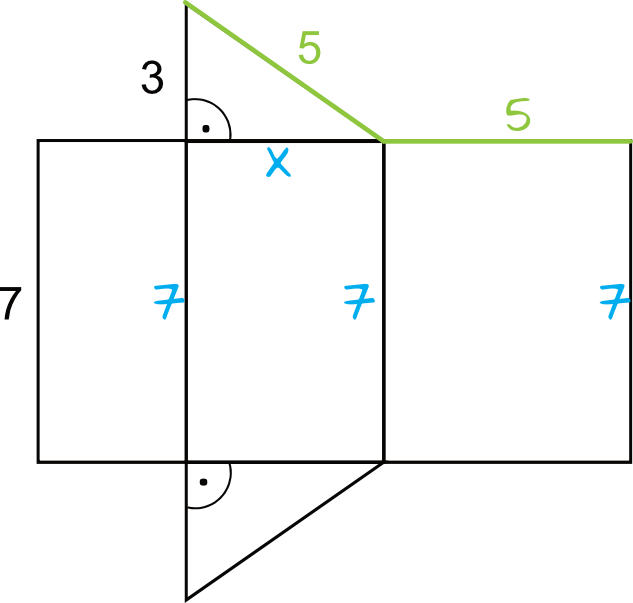
Krok 2. Obliczenie brakującej długości krawędzi graniastosłupa.
Obliczmy od razu brakującą długość krawędzi graniastosłupa (która przyda nam się w jednym z kolejnych kroków).
$$3^2+x^2=5^2 \\
9+x^2=25 \\
x^2=16 \\
x=4 \quad\lor\quad x=-4$$
Ujemną długość oczywiście odrzucamy, zatem zostaje nam \(x=4\).
Krok 3. Ocena prawdziwości pierwszego zdania.
Największą ścianą boczną jest prostokąt o wymiarach \(7\times5\), zatem jego pole powierzchni będzie równe:
$$P=7\cdot5 \\
P=35$$
To oznacza, że zdanie jest prawdą.
Krok 4. Ocena prawdziwości drugiego zdania.
W podstawie graniastosłupa mamy trójkąt, którego przyprostokątnymi są boki o długości \(3\) oraz \(4\). Korzystając ze wzoru na pole trójkąta możemy zapisać, że:
$$P=\frac{1}{2}\cdot3\cdot4 \\
P=6$$
Pole podstawy tego graniastosłupa jest równe \(6\), a nie \(12\), a to oznacza, że zdanie jest fałszem.