Rozwiązanie
Krok 1. Obliczenie wymiarów graniastosłupa.
Spójrzmy na odcinek o długości \(48cm\). Składa się on z trzech jednakowych prostokątów, które są ścianami bocznymi naszej bryły (na pewno są one jednakowe, bo graniastosłup jest prawidłowy, czyli wszystkie ściany boczne są takie same). To oznacza, że krótsza długość pojedynczego prostokąta wynosi:
$$48cm:3=16cm$$
To prowadzi nas do wniosku, że w podstawie znajdzie się kwadrat o boku \(16cm\) (musi to być kwadrat, bo graniastosłup jest prawidłowy). Skoro tak, to wysokość bryły będzie równa:
$$41cm-16cm=25cm$$
Dobrze będzie to wszystko widać na rysunku pomocniczym:
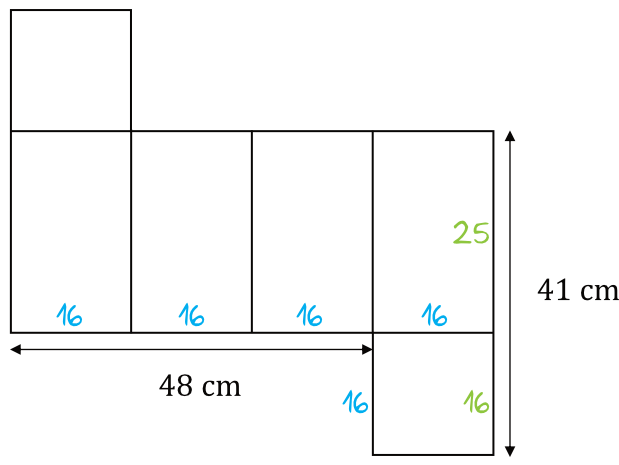
Krok 2. Obliczenie pola podstawy.
W podstawie bryły mamy kwadrat o boku \(16cm\), zatem pole podstawy będzie równe:
$$P_{p}=16cm\cdot16cm \\
P_{p}=256cm^2$$
Krok 3. Obliczenie objętści.
Wiemy już, że \(P_{p}=256cm\) i wyznaczyliśmy sobie, że \(H=25cm\). W związku z tym objętość graniastosłupa będzie równa:
$$V=P_{p}\cdot H \\
V=256cm^2\cdot25 \\
V=6400cm^3$$