Rozwiązanie
Krok 1. Ocena prawdziwości pierwszego zdania.
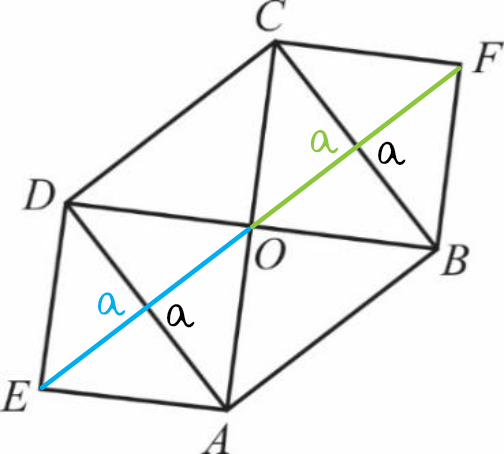
Zwróćmy uwagę, że wszystkie małe trójkąty mają identyczne wymiary oraz identyczne pole powierzchni. Kwadrat \(ABCD\) składa się z czterech takich trójkącików, natomiast każdy z kwadratów \(EAOD\) oraz \(BFCO\) składa się z dwóch trójkącików. Razem więc kwadraty \(EAOD\) oraz \(BFCO\) mają identyczną sumę trójkącików (czyli identyczne pole powierzchni) co kwadrat \(ABCD\). Pierwsze zdanie jest więc prawdą.
Krok 2. Ocena prawdziwości drugiego zdania.
Warto pamiętać, że przekątne kwadratu mają jednakową długość. Jeżeli więc przykładowo przekątna \(AD\) w kwadracie \(EAOD\) ma długość równą boku kwadratu \(ABCD\), to także przekątna \(EO\) musi mieć taką samą długość. Kwadraty \(EAOD\) i \(BFCO\) mają więc łącznie \(4\) przekątne, każda o długości boku kwadratu \(ABCD\), czyli zdanie jest prawdą. Wszelkie wątpliwości rozwieje poniższy rysunek pomocniczy: