Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Poziomą osią układu współrzędnych jest oś iksów. To oznacza, że funkcja \(g\) będzie wyglądać w ten oto sposób:
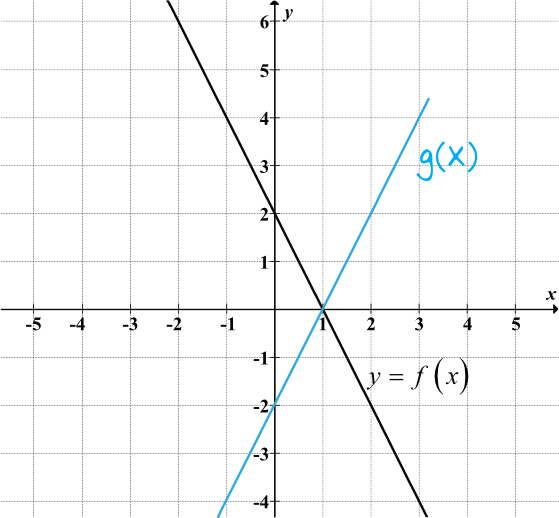
Krok 2. Ustalenie wzoru funkcji \(g(x)\).
Nasza funkcja będzie na pewno wyrażona wzorem w postaci \(g(x)=ax+b\). Musimy tylko ustalić jakie są wartości współczynników \(a\) oraz \(b\). Zacznijmy od ustalenia współczynnika kierunkowego \(a\). Wykres funkcji \(g(x)\) jest prostą rosnącą, zatem współczynnik kierunkowy \(a\) musi być większy od zera. Z tego wynika, że interesują nas już tylko dwie odpowiedzi: B oraz D. Musimy jeszcze ustalić wartość współczynnika \(b\). Współczynnik \(b\) mówi nam o tym w którym miejscu funkcja przecina oś igreków. W naszym przypadku funkcja \(g(x)\) przecina oś igreków dla \(y=-2\), zatem \(b=-2\).
To oznacza, że funkcja \(g\) jest określona wzorem \(g(x)=2x-2\).