Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f(x)=ax^2+bx+c\), o miejscach zerowych: \(-3\) i \(1\).
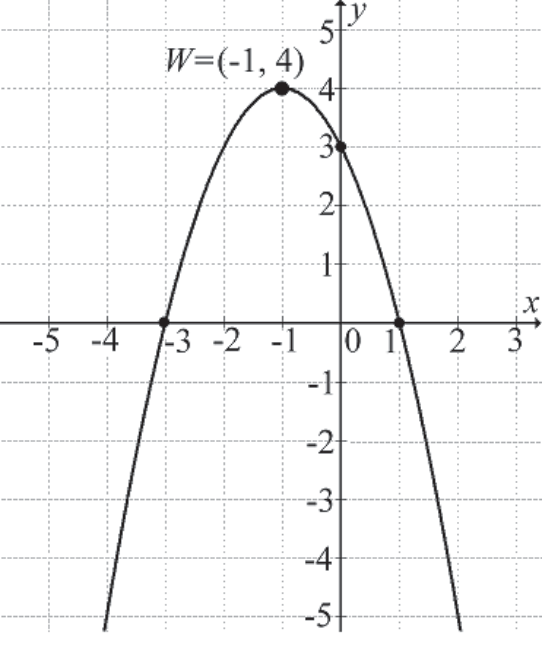
Współczynnik \(c\) we wzorze funkcji \(f\) jest równy:
\(1\)
\(2\)
\(3\)
\(4\)
Rozwiązanie:
Współczynnik \(c\) w postaci ogólnej wzoru funkcji kwadratowej odpowiada miejscu przecięcia się paraboli z osią \(Oy\). Widzimy wyraźnie, że parabola przecina oś \(Oy\) w punkcie o współrzędnych \((0;3)\), zatem współczynnik \(c=3\).
Odpowiedź:
C. \(3\)

