Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Liczenie sumy długości krawędzi patrząc się jedynie na siatkę bryły może być dość problematyczne (istnieje obawa, że pewne krawędzie policzymy podwójnie i tu tkwi największa pułapka w tym zadaniu). Dlatego też dobrze jest zacząć od narysowania sobie szkicu naszego ostrosłupa:
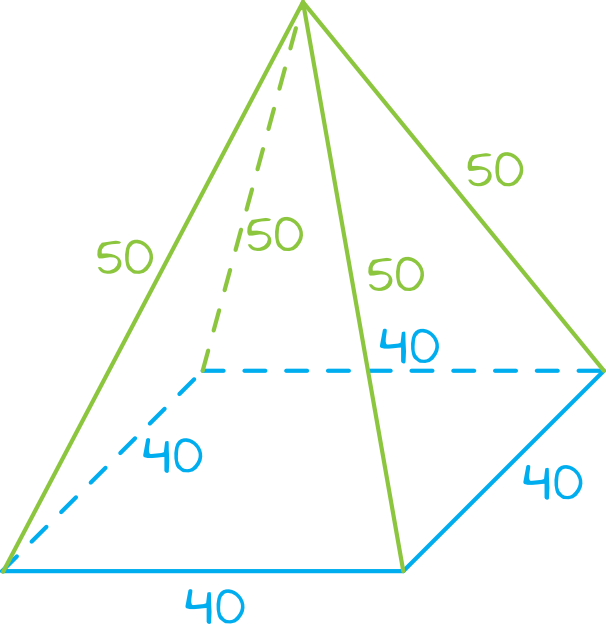
Krok 2. Obliczenie sumy długości krawędzi.
Z rysunku możemy odczytać, że masz ostrosłup prawidłowy czworokątny ma \(4\) krawędzie podstawy oraz \(4\) krawędzie boczne. Skoro krawędź podstawy ma długość \(40cm\), a krawędź boczna \(50cm\), to suma długości wszystkich krawędzi będzie równa:
$$4\cdot40cm+4\cdot50cm=160cm+200cm=360cm$$