Na rysunku przedstawione są dwie proste równoległe \(k\) i \(l\) o równaniach \(y=ax+b\) oraz \(y=mx+n\). Początek układu współrzędnych leży między tymi prostymi.
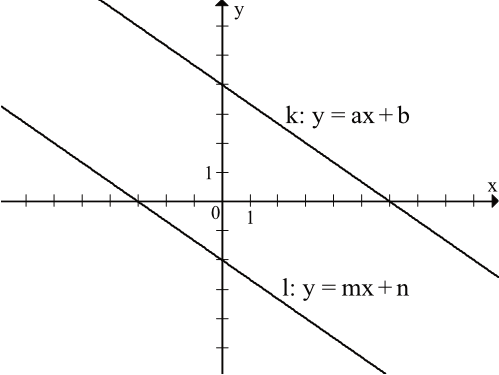
Zatem:
\(a\cdot m\gt0\) i \(b\cdot n\gt0\)
\(a\cdot m\gt0\) i \(b\cdot n\lt0\)
\(a\cdot m\lt0\) i \(b\cdot n\gt0\)
\(a\cdot m\lt0\) i \(b\cdot n\lt0\)
Rozwiązanie:
Krok 1. Ustalenie wartości współczynników \(a\) oraz \(m\).
Obie proste są malejące, a to z kolei oznacza że ich współczynniki kierunkowe (\(a\) oraz \(m\)) są ujemne. Iloczyn liczb ujemnych jest liczbą dodatnią, stąd też \(a\cdot m\gt0\).
Krok 2. Ustalenie wartości współczynników \(b\) oraz \(n\).
Współczynniki \(b\) oraz \(n\) mówią nam w którym miejscu na osi \(y\) przetną się poszczególne proste. Z wykresów możemy odczytać, że pierwsza przecina oś \(Oy\) w dodatnim miejscu, a druga w miejscu ujemnym. To oznacza, że współczynnik \(b\) jest dodatni, natomiast \(n\) jest ujemny. Iloczyn liczby dodatniej i ujemnej jest liczbą ujemną, zatem \(b\cdot n\lt0\).
Podsumowując informacje z pierwszego i drugiego kroku możemy wywnioskować, że prawidłowa jest druga odpowiedź.
Odpowiedź:
B. \(a\cdot m\gt0\) i \(b\cdot n\lt0\)

