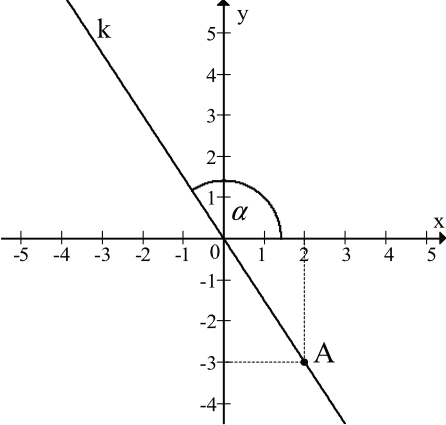
Na rysunku przedstawiona jest prosta \(k\) o równaniu \(y=ax\), przechodząca przez punkt \(A=(2,-3)\) i przez początek układu współrzędnych, oraz zaznaczony jest kąt \(α\) nachylenia tej prostej od osi \(Ox\). Zatem:
\(tgα=-\frac{2}{3}\)
\(tgα=-\frac{3}{2}\)
\(tgα=\frac{2}{3}\)
\(tgα=\frac{3}{2}\)
Rozwiązanie:
Nasz kąt ma swój wierzchołek w początku układu współrzędnych oraz jedno z jego ramion pokrywa się z osią iksów. W takiej sytuacji możemy skorzystać ze wzoru znajdującego w tablicach matematycznych:
$$tgα=\frac{y}{x}$$
\(x\) oraz \(y\) to współrzędne punktu, przez który przechodzi prosta \(k\) będąca ramieniem zaznaczonego kąta. W naszym przypadku podstawimy więc współrzędne punktu \(A\), czyli \(x=2\) oraz \(y=-3\):
$$tgα=\frac{-3}{2}=-\frac{3}{2}$$
Odpowiedź:
B. \(tgα=-\frac{3}{2}\)

