Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
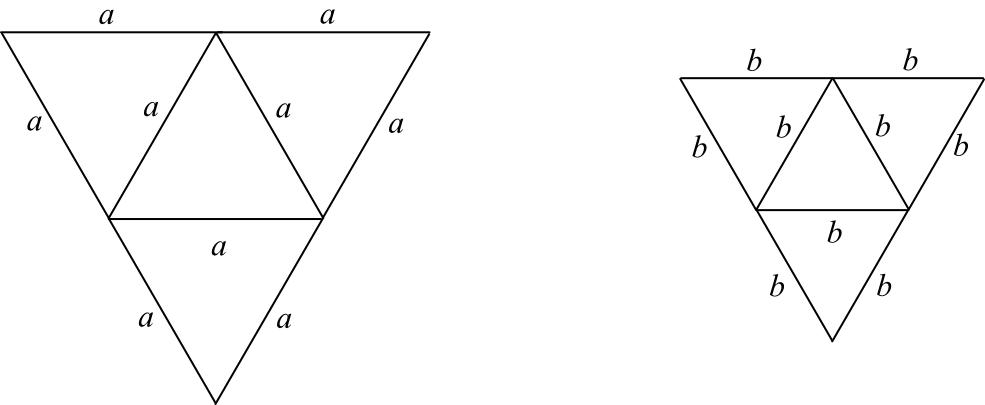
Pole powierzchni całkowitej ostrosłupa o krawędzi \(a\) jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi \(b\). Ile razy objętość ostrosłupa o krawędzi \(a\) jest większa od objętości ostrosłupa o krawędzi \(b\)?
\(\sqrt{2}\)
\(2\)
\(2\sqrt{2}\)
\(4\)
Rozwiązanie:
Zgodnie z zasadą podobieństwa figur, jeśli krawędzie pierwszego ostrosłupa są \(k\) razy większe od drugiego, to pole powierzchni całkowitej pierwszego ostrosłupa jest \(k^2\) większe od pola drugiego, a objętość jest \(k^3\) razy większa.
Krok 1. Obliczenie skali podobieństwa, czyli \(k\).
Wczytując się w treść zadania wiemy, że pole powierzchni całkowitej pierwszego ostrosłupa jest dwa razy większe od pola drugiego ostrosłupa, zatem:
$$k^2=2 \\
k=\sqrt{2}$$
Krok 2. Obliczenie ile razy objętość pierwszego ostrosłupa jest większa od drugiego.
Zgodnie z tym co sobie napisaliśmy na wstępie – objętość pierwszego ostrosłupa będzie \(k^3\) razy większa, zatem:
$$k^3=(\sqrt{2})^3=\sqrt{2}\cdot\sqrt{2}\cdot\sqrt{2}=2\sqrt{2}$$
Odpowiedź:
C. \(2\sqrt{2}\)

