Rozwiązanie
Z treści zadania wynika, że liczby \(k, l, m\) oraz \(n\) są liczbami całkowitymi. Nie musi to oznaczać, że podziałka jest co 1 jednostkę, choć za chwilę sobie udowodnimy, że tak właśnie jest.
Wartość \(\sqrt{41}\) to nieco więcej niż \(\sqrt{36}\) (które jest równe \(6\)) i nieco mniej niż \(\sqrt{49}\) (które jest równe \(7\)). Wartość \(\sqrt{41}\) to w przybliżeniu coś w okolicy \(6,5\). Skoro tak i skoro jedna z podanych liczb jest równa \(0\), to znaczy, że podziałka jest na pewno równa \(1\) (gdyby było inaczej, to żadna z liczb \(k, l, m, n\) nie byłaby równa \(0\)).
To prowadzi nas do wniosku, że sytuacja na osi wygląda następująco:
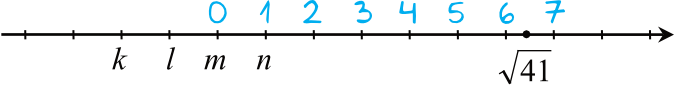
W związku z tym liczbę \(0\) oznaczono na osi jako \(m\).