Na płaszczyźnie dane są punkty \(A=(\sqrt{2},\sqrt{6})\), \(B=(0,0)\) i \(C=(\sqrt{2},0)\). Kąt \(BAC\) jest równy:
\(30°\)
\(45°\)
\(60°\)
\(75°\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Narysujmy sobie układ współrzędnych i oznaczmy na nim (przynajmniej mniej więcej) poszczególne punkty. Pamiętaj, że \(\sqrt{2}\approx1,41\) oraz \(\sqrt{6}\approx2,45\).
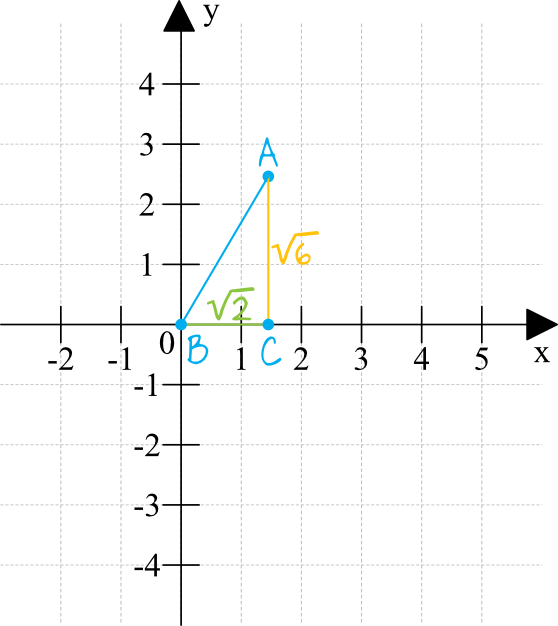
Krok 2. Obliczenie miary kąta.
Powstał nam trójkąt prostokątny w którym znamy tak naprawdę długości dwóch przyprostokątnych:
$$|BC|=\sqrt{2} \\
|AC|=\sqrt{6}$$
Aby obliczyć miarę kąta \(BAC\) możemy skorzystać z funkcji tangensa:
$$tgα=\frac{|BC|}{|AC|} \\
tgα=\frac{\sqrt{2}}{\sqrt{6}} \\
tgα=\frac{\sqrt{2}\cdot\sqrt{6}}{\sqrt{6}\cdot\sqrt{6}} \\
tgα=\frac{\sqrt{12}}{6} \\
tgα=\frac{\sqrt{4\cdot3}}{6} \\
tgα=\frac{2\sqrt{3}}{6} \\
tgα=\frac{\sqrt{3}}{3}$$
Z tablic trygonometrycznych odczytujemy, że tangens przyjmuje wartość \(\frac{\sqrt{3}}{3}\) dla kąta o mierze \(30°\).
Odpowiedź:
A. \(30°\)

