Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Z treści zadania możemy narysować mniej więcej taki oto trójkąt prostokątny:
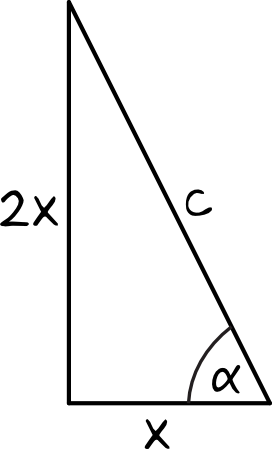
Krok 2. Obliczenie długości przeciwprostokątnej.
Zgodnie z oznaczeniami na rysunku możemy przy pomocy Twierdzenia Pitagorasa zapisać, że:
$$x^2+(2x)^2=c^2 \\
x^2+4x^2=c^2 \\
c^2=5x^2 \\
c=\sqrt{5}x \quad\lor\quad x=-\sqrt{5}x$$
Wartość ujemną odrzucamy, bo długość boku nie może być ujemna, zatem zostaje nam \(c=\sqrt{5}x\).
Krok 3. Obliczenie wartości cosinusa.
Wiedząc, że cosinus to stosunek długości przyprostokątnej leżącej przy kącie \(α\) do przeciwprostokątnej możemy zapisać, że:
$$cosα=\frac{x}{c} \\
cosα=\frac{x}{\sqrt{5}x} \\
cosα=\frac{1}{\sqrt{5}} \\
cosα=\frac{1\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} \\
cosα=\frac{\sqrt{5}}{5}$$