Rozwiązanie
Krok 1. Uproszczenie wyrażenia z dwoma niewiadomymi do wyrażenia z jedną niewiadomą.
Aby móc rozwiązać to zadanie to musimy dojść do sytuacji w której mamy jedną niewiadomą. W tym celu dobrze byłoby wyznaczyć z wyrażenia \(2x+z=1\) niewiadomą \(z\) i podstawić ją potem do wyrażenia \(x^2+z^2+7xz\). W związku z tym:
$$2x+z=1 \\
z=1-2x$$
Podstawiając tę wartość do naszego wyrażenia otrzymamy:
$$x^2+(1-2x)^2+7x\cdot(1-2x)= \\
=x^2+1^2-4x+4x^2+7x-14x^2= \\
=-9x^2+3x+1$$
Krok 2. Interpretacja otrzymanego wyniku.
Otrzymaliśmy wyrażenie, do którego pod iksa możemy podstawiać różne liczby, otrzymując w ten sposób jakieś konkretne wyniki. Możemy więc rozpatrzeć tę sytuację jako klasyczny przykład funkcji, a skoro pojawia nam się tutaj niewiadoma \(x\) podniesiona do kwadratu, to jest to funkcja kwadratowa.
Naszym zadaniem jest teraz dowiedzieć się dla jakiego argumentu \(x\) ta funkcja przyjmie największą wartość, no i musimy podać tę wartość (to jest właśnie istotą tego zadania). Wykresem funkcji kwadratowej jest parabola, a skoro współczynnik kierunkowy \(a\) jest ujemny, bo \(a=-9\), to ramiona tej paraboli będą skierowane do dołu. To oznacza, że ta nasza funkcja będzie więc wyglądać mniej więcej w ten sposób:
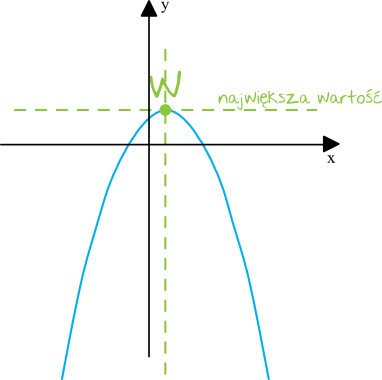
Z tego szkicowego rysunku wynika jasno, że największą wartość ta funkcja przyjmie w swoim wierzchołku. Musimy więc poznać współrzędne tego wierzchołka.
Krok 3. Wyznaczenie współrzędnych wierzchołka paraboli.
Aby wyznaczyć współrzędne wierzchołka paraboli \(W=(p;q)\) posłużymy się wzorami:
$$p=\frac{-b}{2a} \\
q=\frac{-\delta}{4a}$$
Do obliczenia współrzędnej \(q\) potrzebna nam będzie delta, zatem obliczmy ją w tym momencie:
Współczynniki: \(a=-9,\;b=3,\;c=1\)
$$Δ=b^2-4ac=3^2-4\cdot(-9)\cdot1=9-(-36)=9+36=45$$
Znamy więc wartości wszystkich współczynników, znamy też deltę, zatem możemy podstawić te dane do naszych wzorów, otrzymując:
$$p=\frac{-b}{2a} \\
p=\frac{-3}{2\cdot(-9)} \\
p=\frac{-3}{-18} \\
p=\frac{1}{6}$$
$$q=\frac{-45}{4\cdot(-9)} \\
q=\frac{-45}{-36} \\
q=\frac{5}{4}$$
Wyszło nam więc, że wierzchołek tej paraboli znajduje się w punkcie \(W=\left(\frac{1}{6};\frac{5}{4}\right)\). To oznacza, że największą możliwą wartością tej funkcji (a tym samym naszego wyrażenia) jest wartość \(\frac{5}{4}\).
Znamy też już jedną z niewiadomych wchodzących w skład tego wyrażenia, czyli wiemy że \(x=\frac{1}{6}\). Musimy jeszcze tylko wyznaczyć wartość niewiadomej \(z\).
Krok 4. Obliczenie wartości niewiadomej \(z\).
Korzystając z informacji, że \(2x+z=1\) oraz wiedząc, że \(x=\frac{1}{6}\) otrzymamy:
$$2\cdot\frac{1}{6}+z=1 \\
\frac{1}{3}+z=1 \\
z=\frac{2}{3}$$