Rozwiązanie
Krok 1. Wyznaczenie współrzędnej \(p\) wierzchołka paraboli.
Wykresem funkcji kwadratowej jest zawsze parabola. Jedną z własności parabol jest to, że jej wierzchołek znajduje się zawsze w równej odległości od argumentów o jednakowej wartości (zwyczajowo mówimy, że wierzchołek znajduje się dokładnie między miejscami zerowymi, choć ta zależność dotyczy tak naprawdę nie tylko miejsc zerowych).
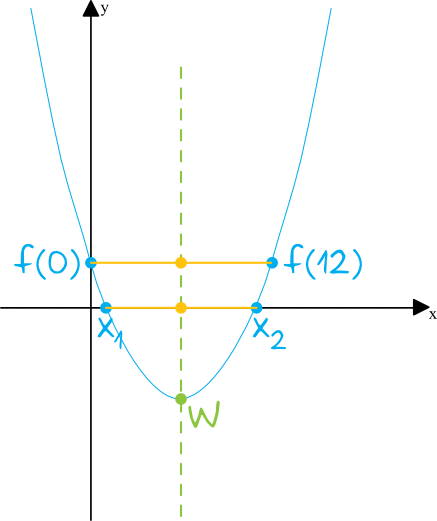
Możemy więc zapisać, że:
$$p=\frac{0+12}{2} \\
p=\frac{12}{2} \\
p=6$$
Krok 2. Wyznaczenie drugiego miejsca zerowego.
Teraz skorzystamy z dokładnie tej samej własności co przed chwilą, tylko w drugą stronę. Odległość od pierwszego miejsca zerowego do wierzchołka jest taka sama jak od wierzchołka do drugiego miejsca, czyli:
$$\frac{x_{1}+x_{2}}{2}=p \\
\frac{4+x_{2}}{2}=6 \\
4+x_{2}=12 \\
x_{2}=8$$
Krok 3. Zapisanie wzoru funkcji w postaci iloczynowej.
Znając wszystkie miejsca zerowe, możemy przystąpić do zapisania wzoru funkcji w postaci iloczynowej:
$$y=a(x-x_{1})(x-x_{2}) \\
y=a(x-4)(x-8)$$
Brakuje nam jeszcze znajomości współczynnika \(a\). Możemy skorzystać z informacji, że np. \(f(0)=2\), czyli że dla argumentu \(x=0\) funkcja przyjmuje wartość \(y=2\). Podstawiając zatem te współrzędne do wyznaczonej postaci iloczynowej, otrzymamy:
$$2=a\cdot(0-4)\cdot(0-8) \\
2=a\cdot(-4)\cdot(-8) \\
2=32a \\
a=\frac{1}{16}$$
To oznacza, że pełnym wzorem tej funkcji w postaci iloczynowej jest:
$$y=\frac{1}{16}(x-4)(x-8)$$
Krok 4. Wyznaczenie najmniejszej wartości funkcji.
Funkcja ma ramiona skierowane do góry (bo współczynnik \(a\) jest dodatni), więc najmniejsza wartość tej funkcji jest przyjmowana w wierzchołku. Nie będziemy tutaj korzystać ze wzoru na współrzędną \(q\), czyli \(q=\frac{-Δ}{4a}\), bo nie mamy postaci ogólnej. Możemy postąpić sprytniej i obliczyć wartość funkcji dla \(x=6\), czyli właśnie wartość przyjmowaną w wierzchołku:
$$y=\frac{1}{16}\cdot(6-4)\cdot(6-8) \\
y=\frac{1}{16}\cdot2\cdot(-2) \\
y=\frac{1}{16}\cdot(-4) \\
y=-\frac{1}{4}$$