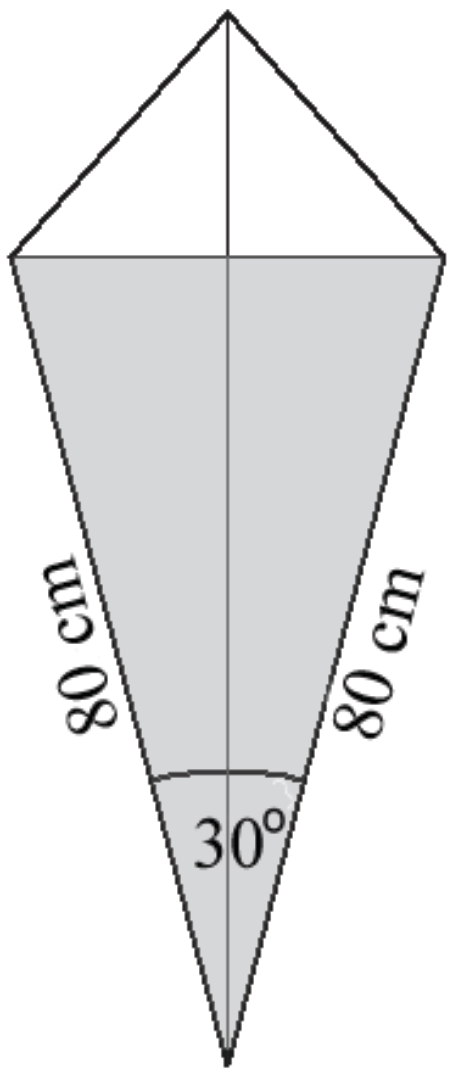
Latawiec ma wymiary podane na rysunku. Powierzchnia zacieniowanego trójkąta jest równa

$3200cm^2$

$6400cm^2$

$1600cm^2$

$800cm^2$

Rozwiązanie:

W tym zadaniu skorzystamy ze wzoru na pole trójkąta: $P=\frac{1}{2}a\cdot b\cdot sinα$.

Krok 1. Wypisanie danych z zadania, potrzebnych do obliczeń.

Pierwszy bok trójkąta: $a=80cm$
Drugi bok trójkąta: $b=80cm$
Sinus kąta między bokami trójkąta: $sin30°=\frac{1}{2}$

Krok 2. Obliczenie pola trójkąta.

$$P=\frac{1}{2}a\cdot b\cdot sinα \\
P=\frac{1}{2}\cdot80cm\cdot80cm\cdot\frac{1}{2} \\
P=1600cm^2$$

Odpowiedź:

C. $1600cm^2$