Kwadrat \(K_{1}\) ma bok długości \(a\). Obok niego rysujemy kolejno kwadraty \(K_{2}, K_{3}, K_{4},…\) takie, że kolejny kwadrat ma bok połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
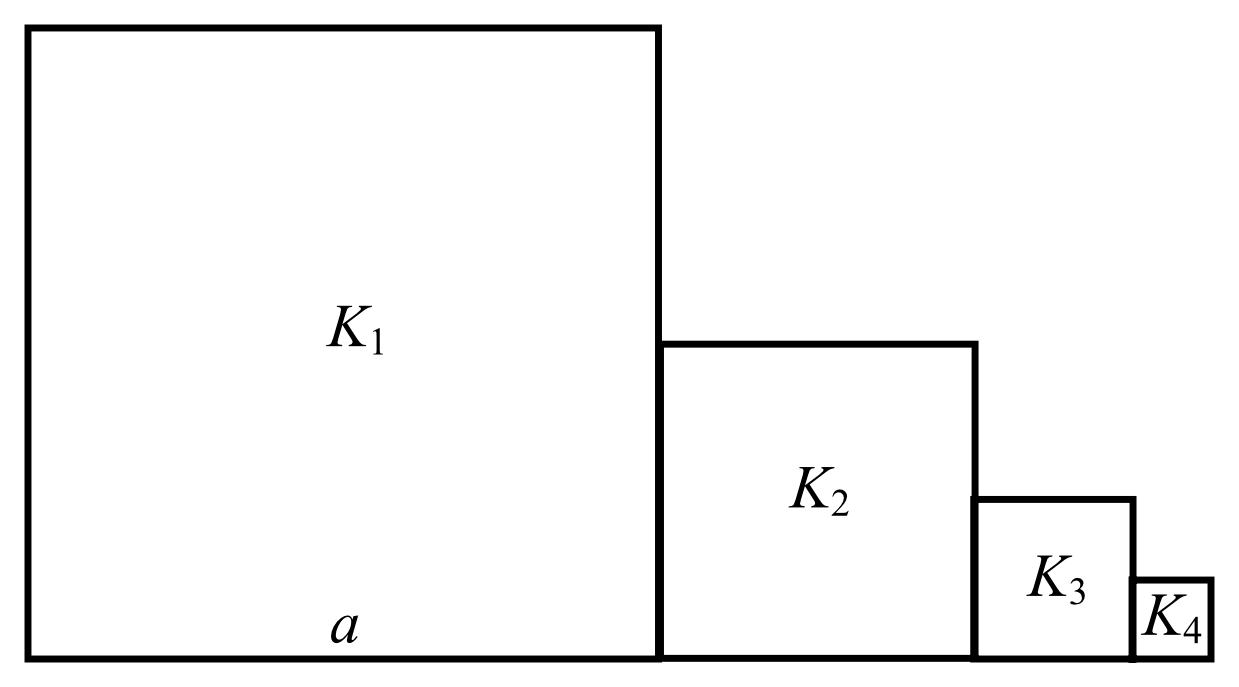
Wyznacz pole kwadratu \(K_{12}\).
Rozwiązanie:
Krok 1. Wyznaczenie długości boku kwadratu \(K_{12}\).
Pierwszy kwadrat ma długość boku równą \(a\).
Drugi kwadrat ma długość boku równą \(\frac{a}{2}\).
Trzeci kwadrat ma długość boku równą \(\frac{a}{2^2}\).
Czwarty kwadrat ma długość boku równą \(\frac{a}{2^3}\).
…
Dwunasty kwadrat ma długość boku równą \(\frac{a}{2^{11}}\).
Krok 2. Obliczenie pola kwadratu \(K_{12}\).
Podstawiając do wzoru na pole kwadratu długość boku równą \(\frac{a}{2^{11}}\) otrzymamy:
$$P=\left(\frac{a}{2^{11}}\right)^2=\frac{a^2}{2^{22}}$$
Odpowiedź:
\(P=\frac{a^2}{2^{22}}\)


Czy odpowiedz P = a^2 * (1/4)^11 była by akceptowalna na maturze?
Pewnie, to bardzo dobry zapis :)