Koła i okręgi - zadania (egzamin ósmoklasisty)
Zadanie 1. (1pkt) Rysunek przedstawia ślad na śniegu, który pozostawił jadący na nartach Adam.
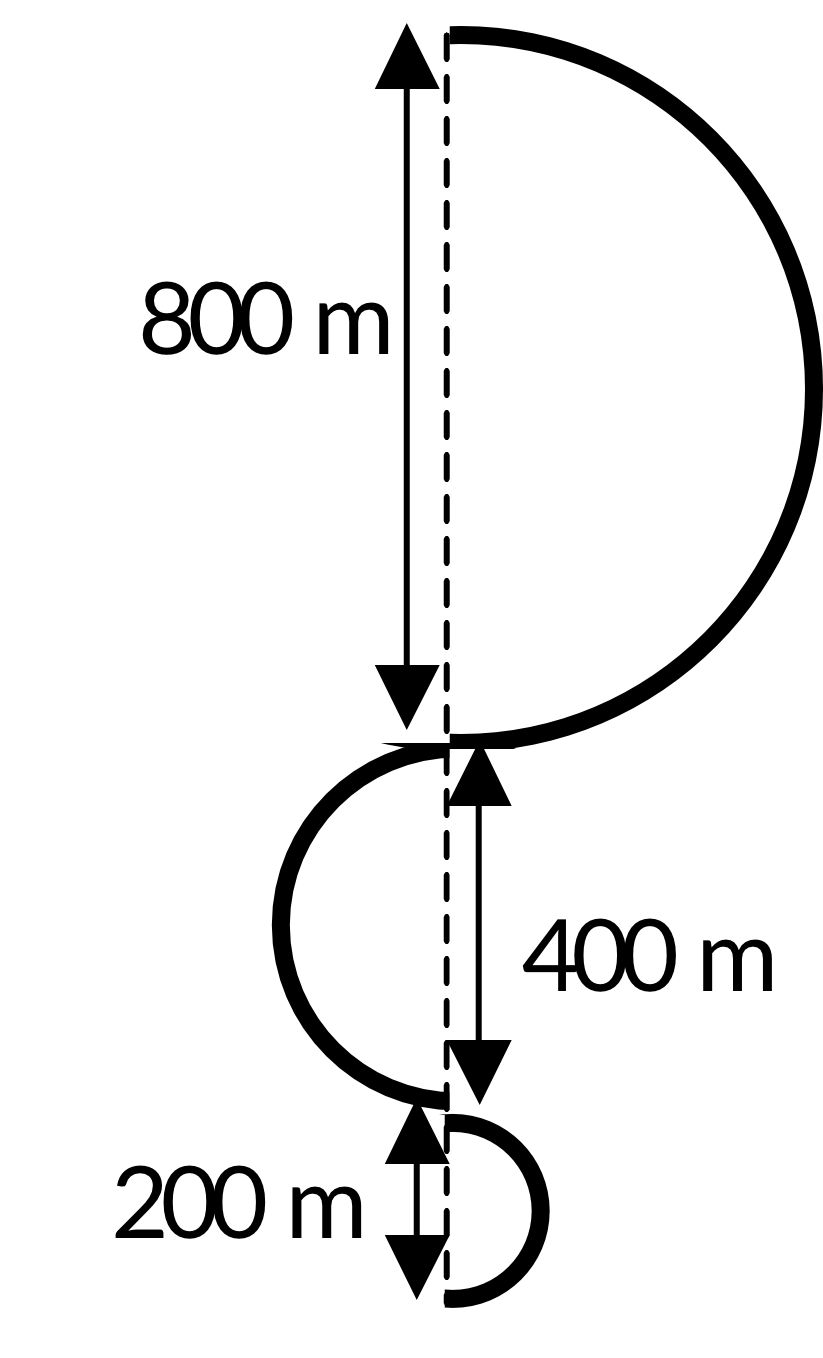
Długość trasy przebytej przez Adama równa jest:
Wyjaśnienie:
Krok 1. Analiza rysunku.
Zauważmy, że ślad na śniegu składa się tak naprawdę z trzech części, z których każda jest połową obwodu jakiegoś okręgu. Pierwszy łuk jest połową okręgu o średnicy \(800m\), drugi łuk jest połową okręgu o średnicy \(400m\), a trzeci łuk jest połową okręgu o średnicy \(200m\).
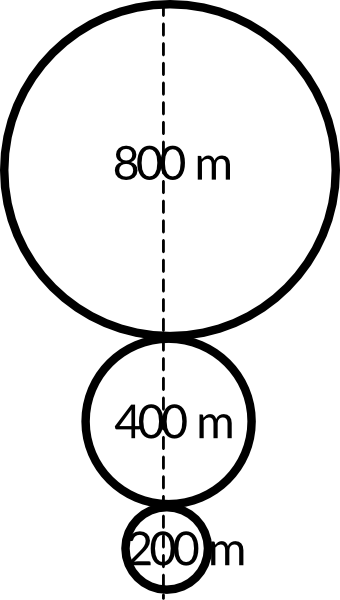
Krok 2. Obliczenie połówek obwodu każdego z trzech okręgów.
Wiemy już, że jak poznamy długości trzech obwodów okręgów (a w zasadzie ich połówek) to w prosty sposób dojdziemy do rozwiązania zadania. Wzór na obwód okręgu jest następujący:
$$Obw=2πr$$
Skoro potrzebujemy długości połowy okręgu, to możemy nawet zapisać, że wzór na pojedynczy łuk to:
$$Łuk=\frac{1}{2}\cdot2πr=πr$$
I tu uwaga, bo ukryła się tutaj największa pułapka. We wzorze musimy skorzystać z promienia okręgu, natomiast my na rysunku mamy zaznaczone średnice! Promień jest dwa razy mniejszy od średnicy, zatem:
I łuk: \(r=400m\)
II łuk: \(r=200m\)
III łuk: \(r=100m\)
Teraz możemy przystąpić do obliczeń:
I łuk: \(πr=400π\;m\)
II łuk: \(πr=200π\;m\)
III łuk: \(πr=100π\;m\)
Krok 3. Obliczenie długości trasy.
Suma trzech łuków jest poszukiwaną przez nas długością trasy, zatem:
$$400π\;m+200π\;m+100π\;m=700π\;m$$
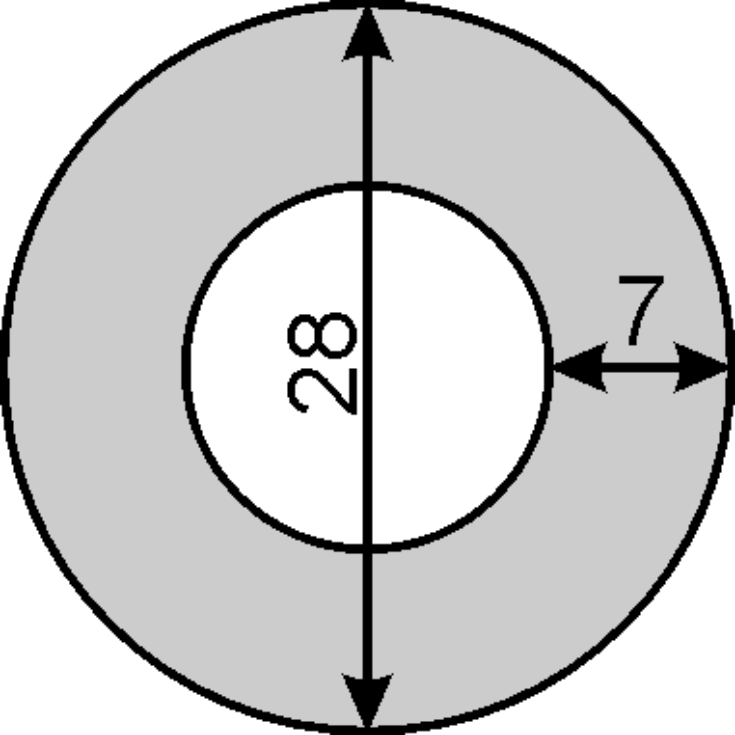
Zadanie 2. (5pkt) Na miejscu dawnego skrzyżowania postanowiono wybudować rondo, którego wymiary (w metrach) podane są na rysunku. Oblicz, na jakiej powierzchni trzeba wylać asfalt (obszar zacieniowany na rysunku). W swoich obliczeniach za \(π\) podstaw \(\frac{22}{7}\).
Odpowiedź
Asfalt trzeba wylać na powierzchni \(462m^2\).
Wyjaśnienie:
Całość zadania sprowadza się tak naprawdę do tego by obliczyć pola dwóch kół - dużego i małego. Poszukiwany obszar (pierścień) będzie właśnie różnicą powierzchni między kołem dużym i małym.
Krok 1. Obliczenie pola powierzchni dużego koła.
Skorzystamy ze wzoru:
$$P=πr^2$$
Widzimy, że do obliczenia pola koła potrzebny jest nam promień, a my na rysunku mamy podaną średnicę równą \(28cm\). Z racji tego iż promień jest dwukrotnie mniejszy od średnicy, to \(r=14cm\). Teraz możemy podstawić już te dane do wzoru, od razu stosując proponowane przybliżenie \(π=\frac{22}{7}\):
$$P=\frac{22}{7}\cdot(14m)^2 \\
P=\frac{22}{7}\cdot196m^2 \\
P=616m^2$$
Krok 2. Obliczenie pola powierzchni małego koła.
Ponownie musimy podstawić dane do wzoru na pole koła, ale musimy jeszcze ustalić jaka jest długość promienia tego małego koła. Przyglądając się rysunkowi widzimy wyraźnie, że aby obliczyć długość tego promienia musimy od promienia dużego koła odjąć szerokość pierścienia. Otrzymamy zatem:
$$r=14m-7m=7m$$
Znając długość promienia podstawiamy go ponownie do wzoru na pole koła:
$$P=\frac{22}{7}\cdot(7m)^2 \\
P=\frac{22}{7}\cdot49m^2 \\
P=154m^2$$
Krok 3. Obliczenie pola powierzchni ronda.
Znając pola powierzchni dużego i małego koła bez problemu obliczymy pole pierścienia, czyli naszego ronda:
$$P=616m^2-154m^2=462m^2$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz jedynie promienie obydwu kół jako \(r=7\) oraz \(R=14\).
2 pkt
• Gdy poprawnie obliczysz pole jednego z kół (Krok 1. lub 2.).
3 pkt
• Gdy poprawnie obliczysz pole obydwu kół (Krok 1. i 2.).
4 pkt
• Gdy obliczysz pole powierzchni ronda (Krok 3.), ale nie zapiszesz w końcowym wyniku poprawnej jednostki.
5 pkt
• Gdy otrzymasz oczekiwany wynik.
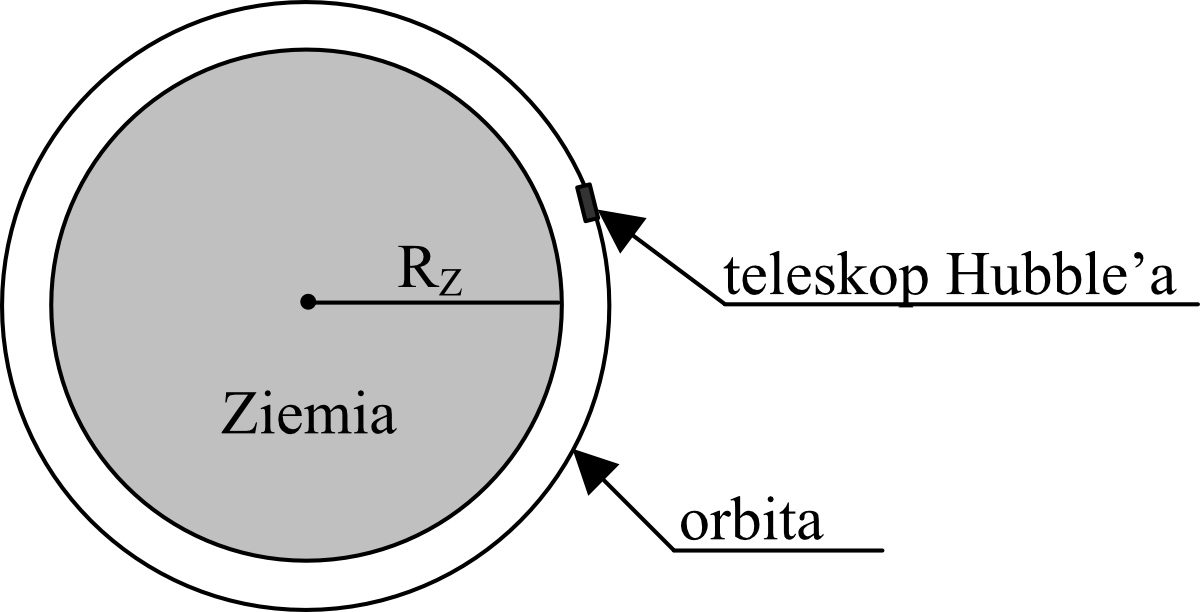
Zadanie 3. (3pkt) Teleskop Hubble’a znajduje się na orbicie okołoziemskiej na wysokości około \(600km\) nad Ziemią. Oblicz wartość prędkości, z jaką porusza się on wokół Ziemi, jeżeli czas jednego okrążenia Ziemi wynosi około \(100\) minut.
(Przyjmij \(R_{z}=6400km, π=\frac{22}{7}\))
Odpowiedź
Teleskop porusza się z prędkością \(v=26400\frac{km}{h}\).
Wyjaśnienie:
Krok 1. Obliczenie promienia okręgu po którym porusza się teleskop.
Do obliczenia prędkości (a to jest celem naszego zadania) będziemy potrzebować drogi i czasu. Czas jest podany, musimy więc wyznaczyć drogę. Nasza droga (czyli orbita) jest tak naprawdę obwodem pewnego okręgu, zatem jej długość możemy wyliczyć ze wzoru:
$$Obw=2πr$$
Potrzebujemy więc ustalić najpierw jaka jest ta długość promienia. Nie będzie to \(6400km\), bo to jest jedynie promień Ziemi, a teleskop znajduje się jeszcze wyżej. To oznacza, że do wartości \(R_{z}=6400km\) musimy dodać wysokość na jakiej wzniósł się teleskop, czyli \(600km\). Otrzymamy w ten sposób promień okręgu, który jest naszą orbitą.
$$r=6400km+600km=7000km$$
Krok 2. Obliczenie długości okręgu/orbity.
Znając promień bez problemu wyznaczymy długość orbity. Od razu też użyjemy przybliżenia liczby \(π\), które jest podane w treści zadania:
$$Obw=2π\cdot7000km \\
Obw=14000π\;km \\
Obw=14000\cdot\frac{22}{7}km \\
Obw=44000km$$
Krok 3. Obliczenie prędkości poruszania się teleskopu wokół Ziemi.
Prędkość poruszania się teleskopu obliczymy ze wzoru:
$$v=\frac{s}{t}$$
Długość drogi obliczyliśmy w poprzednim kroku, czas jest podany w treści zadania, więc bez problemu możemy przystąpić do obliczeń. Co prawda w treści zadania nie mamy podane w jakiej jednostce mamy podać tę prędkość (najłatwiej byłoby ją podać w \(\frac{km}{min}\)), ale spróbujmy ją podać w najbardziej typowej jednostce czyli w \(\frac{km}{h}\). Musimy więc jeszcze zapisać, że:
$$100min=1\frac{2}{3}h=\frac{5}{3}h$$
W związku z tym prędkość poruszania się teleskopu jest równa:
$$v=\frac{44000km}{\frac{5}{3}h}$$
Kreska ułamkowa jest formą dzielenia, więc aby wybrnąć z tego niewygodnego zapisu najprościej będzie to dzielenie zastąpić tak zwanym mnożeniem przez odwrotność:
$$v=44000km\cdot\frac{3}{5}h \\
v=26400\frac{km}{h}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie określisz długość promienia okręgu, po którym porusza się teleskop (Krok 1.).
2 pkt
• Gdy obliczysz długość okręgu i prędkość, ale popełnisz błąd rachunkowy.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 4. (1pkt) Kształt i wymiary deski do krojenia przedstawiono na rysunku.
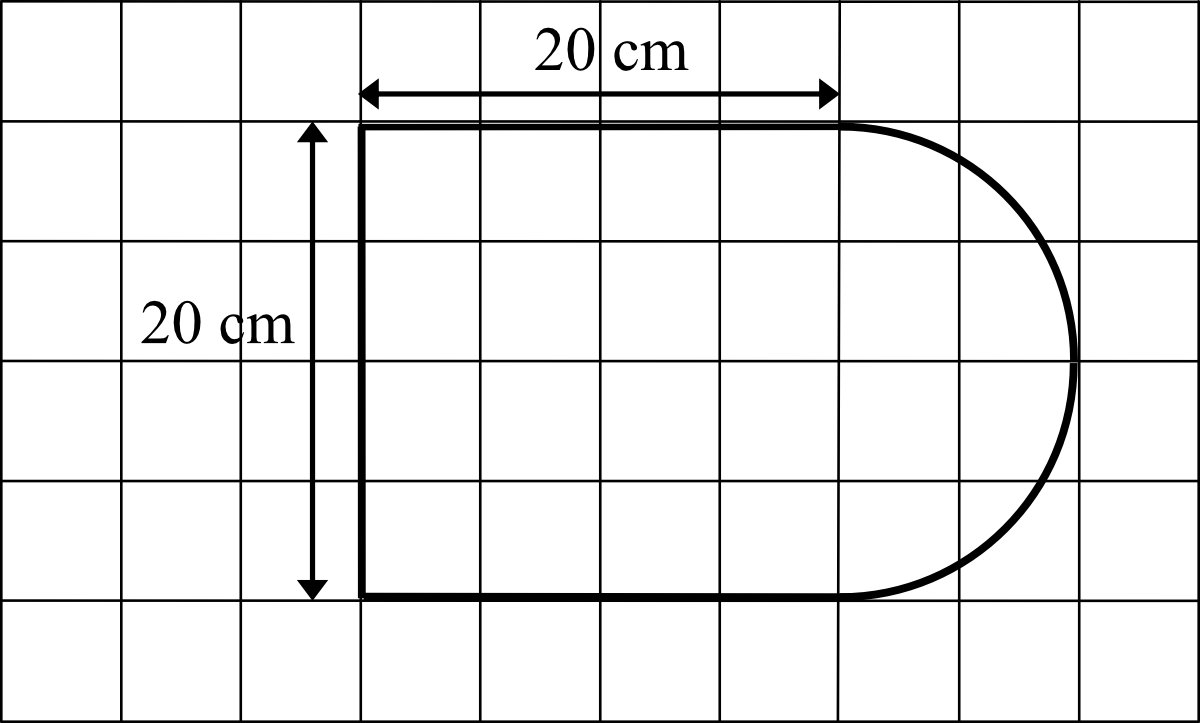
Powierzchnia tej deski (w \(cm^2\)) jest równa:
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Deska sama w sobie ma dość nietypowy kształt, zatem jej powierzchni nie obliczymy ot tak podstawiając coś do wzoru na powierzchnię. Możemy jednak dostrzec, że dałoby się podzielić tę deskę na dwie różne figury, których pola będą możliwe do policzenia - kwadrat oraz połowa koła.
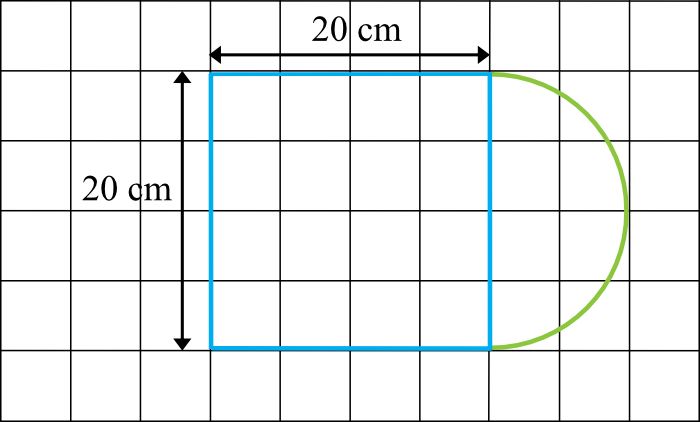
Krok 2. Obliczenie pola kwadratu.
Pierwszą figurą jest kwadrat o boku \(20cm\), zatem jego pole powierzchni będzie równe:
$$P=20cm\cdot20cm=400cm^2$$
Krok 3. Obliczenie pola połowy koła.
Drugą częścią naszej deski jest połowa koła. Jednak najpierw policzymy pole całego koła, a dopiero potem podzielimy sobie otrzymany wynik przez dwa. Wzór na pole koła jest następujący:
$$P=πr^2$$
Do obliczenia pola koła potrzebujemy znać długość promienia okręgu. Z rysunku widać, że każda kratka ma długość \(5cm\), zatem skoro promień okręgu ma długość dwóch kratek, to \(r=10cm\). To oznacza, że pole okręgu jest równe:
$$P=π\cdot(10cm)^2 \\
P=100πcm^2$$
Zgodnie z naszą analizą potrzebujemy połowy pola naszego koła. Zatem interesująca nas część będzie miała pole
$$P=100πcm^2:2=50πcm^2$$
Krok 4. Obliczenie pola powierzchni deski.
Pole deski jest sumą pola kwadratu oraz połówki koła, zatem:
$$P=400cm^2+50πcm^2$$