Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Z treści zadania wynika, że w podstawie mamy trójkąt równoboczny, a ostrosłup wygląda mniej więcej w ten oto sposób:
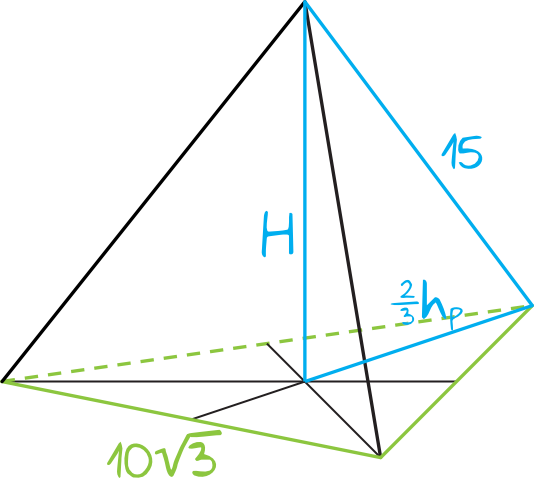
Krok 2. Obliczenie wysokości trójkąta znajdującego się w podstawie.
Skoro w podstawie mamy trójkąt równoboczny, to jego wysokość obliczymy korzystając ze wzoru:
$$h=\frac{a\sqrt{3}}{2}$$
Podstawiając do tego wzoru \(a=10\sqrt{3}\), otrzymamy:
$$h_{p}=\frac{10\sqrt{3}\cdot\sqrt{3}}{2} \\
h_{p}=\frac{10\cdot3}{2} \\
h_{p}=\frac{30}{2} \\
h_{p}=15$$
Tym samym odcinek o długości \(\frac{2}{3}h_{p}\) będzie miał długość \(\frac{2}{3}\cdot15=10\).
Krok 3. Obliczenie wysokości ostrosłupa.
Spójrzmy na nasz kluczowy trójkąt prostokątny, który tworzą odcinek o długości \(\frac{2}{3}h\), wysokość ostrosłupa oraz krawędź boczna. Znamy dwie długości boków tego trójkąta, zatem możemy skorzystać z Twierdzenia Pitagorasa:
$$10^2+H^2=15^2 \\
100+H^2=225 \\
H^2=125 \\
H=\sqrt{125} \quad\lor\quad H=-\sqrt{125}$$
Ujemny wynik oczywiście odrzucamy, ponieważ wysokość ostrosłupa musi być dodatnia. Stąd też zostaje nam jedynie \(H=\sqrt{125}\), co możemy jeszcze rozpisać jako \(H=\sqrt{25\cdot5}=5\sqrt{5}\).