Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
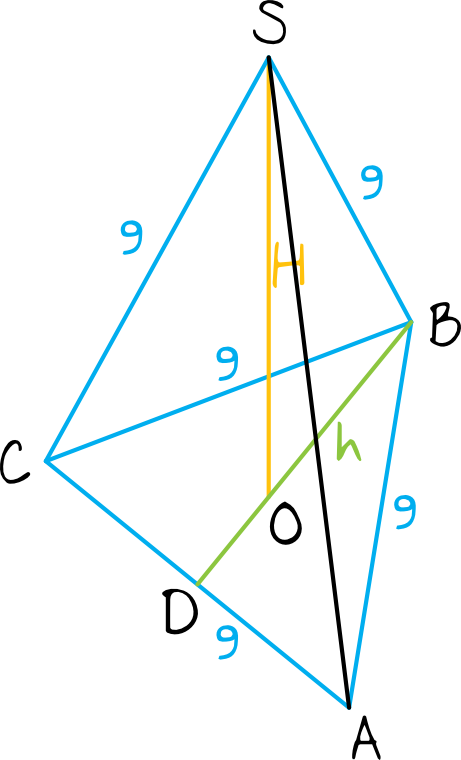
Krok 2. Obliczenie długości odcinka \(BD\).
Odcinek \(BD\) jest wysokością trójkąta równobocznego o boku \(a=9\), zatem:
$$|BD|=\frac{a\sqrt{3}}{2} \\
|BD|=\frac{9\sqrt{3}}{2}$$
Krok 3. Obliczenie długości odcinka \(BO\).
Wysokość ostrosłupa prawidłowego trójkątnego dzieli nam odcinek \(BD\) na dwa części z których odcinek \(BO=\frac{2}{3}BD\) oraz \(DO=\frac{1}{3}BD\) (wynika to wprost z własności trójkątów równobocznych). Nas interesuje długość odcinka \(BO\), zatem:
$$|BO|=\frac{2}{3}\cdot\frac{9\sqrt{3}}{2} \\
|BO|=\frac{18\sqrt{3}}{6} \\
|BO|=3\sqrt{3}$$
Krok 4. Obliczenie długości odcinka \(OS\).
Teraz korzystając z Twierdzenia Pitagorasa w trójkącie \(OBS\) możemy obliczyć wysokość bryły, czyli długość odcinka \(OS\):
$$|OB|^2+|OS|^2=|SB|^2 \\
(3\sqrt{3})^2+|OS|^2=9^2 \\
9\cdot3+|OS|^2=81 \\
27+|OS|^2=81 \\
|OS|^2=54 \\
|OS|=\sqrt{54} \quad\lor\quad |OS|=-\sqrt{54}$$
Wartość ujemną odrzucamy, bo odcinek nie może mieć ujemnej długości, zatem zostaje nam:
$$|OS|=\sqrt{54}=\sqrt{9\cdot6}=3\sqrt{6}$$