Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W tym zadaniu trzeba pamiętać, że przekątne rombu przecinają się w połowie swojej długości pod kątem prostym oraz że dzielą nam kąty rozwarte na dwie równe miary. W związku z tym całość wyglądać będzie w następujący sposób:
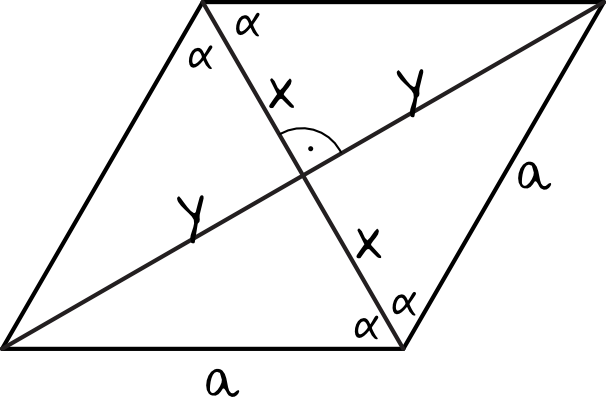
Krok 2. Ułożenie układu równań.
Z treści zadania wiemy, że suma długości przekątnych jest równa \(68\), czyli zgodnie z naszym rysunkiem:
$$2x+2y=68$$
Dodatkowo wiemy, że tangens kąta \(α\) jest równy \(2,4\). Tangens opisuje zależność między przyprostokątną leżącą naprzeciwko kąta \(α\) do przyprostokątnej leżącej przy tym kącie, zatem:
$$tgα=2,4 \\
\frac{y}{x}=2,4$$
I to właśnie z tych dwóch równań możemy ułożyć układ równań:
\begin{cases}
2x+2y=68 \\
\frac{y}{x}=2,4
\end{cases}
Krok 3. Rozwiązanie układu równań.
Najprościej będzie rozwiązać ten układ równań metodą podstawiania. W tym celu możemy wyznaczyć np. wartość igreka z drugiego równania i podstawić go do równania pierwszego:
$$\begin{cases}
2x+2y=68 \quad\bigg/:2 \\
\frac{y}{x}=2,4 \quad\bigg/\cdot x
\end{cases}$$
$$\begin{cases}
x+y=34 \\
y=2,4x
\end{cases}$$
Podstawiając teraz drugie równanie do pierwszego otrzymamy:
$$x+2,4x=34 \\
3,4x=34 \\
x=10$$
Znając wartość \(x=10\) możemy obliczyć brakującą wartość igreka, podstawiając iksa do jednego z równań:
$$10+y=34 \\
y=24$$
Krok 4. Obliczenie długości boku rombu.
Spójrzmy na jeden z czterech trójkątów prostokątnych, które powstały nam w rombie. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$x^2+y^2=a^2 \\
10^2+24^2=a^2 \\
100+576=a^2 \\
a^2=676 \\
a=26 \quad\lor\quad a=-26$$
Wartość ujemną oczywiście odrzucamy, zatem zostaje nam \(a=26\).
Krok 5. Obliczenie obwodu rombu.
Samo obliczenie obwodu jest już formalnością, bo już wiemy że nasz romb ma cztery boki o długości \(26\), zatem:
$$Obw=4\cdot26 \\
Obw=104$$