Kąt rozwarcia stożka ma miarę \(120°\), a tworząca tego stożka ma długość \(6\). Promień podstawy stożka jest równy:
\(3\)
\(6\)
\(3\sqrt{3}\)
\(6\sqrt{3}\)
Rozwiązanie:
Spróbujmy stworzyć rysunek poglądowy:
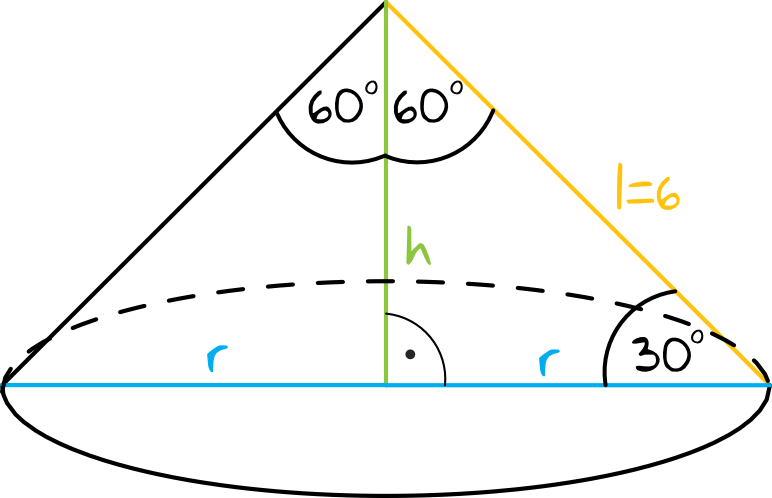
Kiedy naniesiemy sobie wszystkie dane z treści zadania na szkic rysunku to okaże się, że tak naprawdę musimy obliczyć długość podstawy trójkąta prostokątnego. To oznacza, że będziemy mogli skorzystać z funkcji trygonometrycznych albo też z własności trójkątów \(30°,60°,90°\). Zatem:
$$\frac{r}{6}=sin60° \\
\frac{r}{6}=\frac{\sqrt{3}}{2} \\
r=3\sqrt{3}$$
Odpowiedź:
C. \(3\sqrt{3}\)

