Kąt \(CAB\) trójkąta prostokątnego \(ACB\) ma miarę \(30°\). Pole kwadratu \(DEFG\), wpisanego w ten trójkąt (zobacz rysunek) jest równe \(4\). Oblicz pole trójkąta \(ACB\).
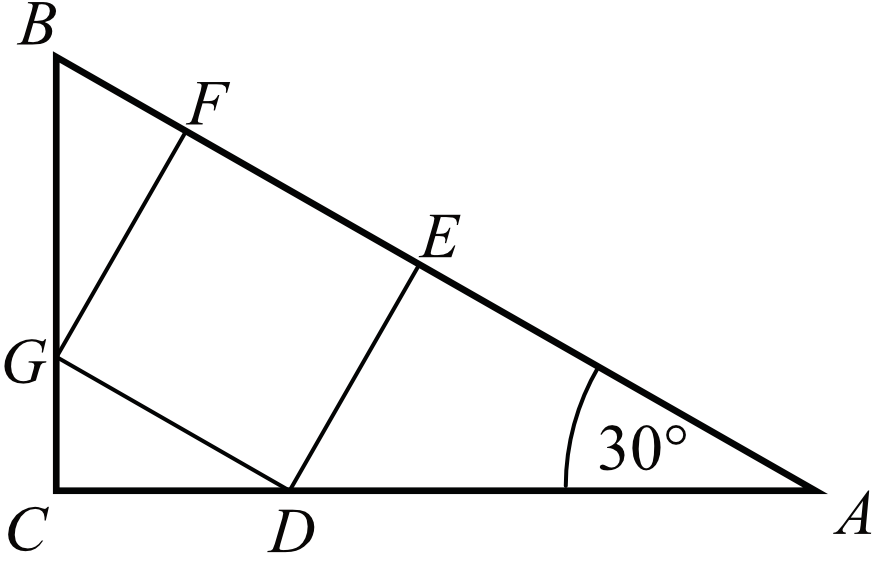
Rozpatrzmy sobie trzy małe trójkąty: \(DAE\), \(CDG\) oraz \(GFB\).
– każdy z nich jest prostokątny, co do tego nie mamy chyba wątpliwości.
– skoro \(|\sphericalangle DAE|=30°\) to \(|\sphericalangle EDA|=60°\) (bo suma kątów w trójkącie \(DAE\) musi być równa \(180°\)).
– skoro \(|\sphericalangle EDA|=60°\) oraz \(|\sphericalangle GDE|=90°\), to z kątów przyległych widzimy że \(|\sphericalangle CDG|=30°\).
– skoro \(|\sphericalangle CDG|=30°\) to \(|\sphericalangle CGD|=60°\) (bo suma kątów w trójkącie \(CDG\) musi być równa \(180°\)).
– skoro \(|\sphericalangle CGD|=60°\) oraz \(|\sphericalangle FGD|=90°\), to z kątów przyległych widzimy że \(|\sphericalangle BGF|=30°\).
– skoro \(|\sphericalangle BGF|=30°\) to \(|\sphericalangle GBF|=60°\) (bo suma kątów w trójkącie \(GFB\) musi być równa \(180°\)).
Wszystkie te trójkąty mają więc miary kątów równe \(30°, 60°, 90°\).
Dodatkowo każdy z tych trójkątów ma długość jednego z boków równą \(2\), bo skoro pole kwadratu jest równe \(4\), to:
$$|GD|=|DE|=|FE|=|GF|=2$$
Wszystkie te długości możemy obliczyć albo wykorzystując cechy trójkątów \(30°, 60°, 90°\), albo wykorzystując funkcje trygonometryczne.
a) Obliczenie długości \(|DA|\)
$$\frac{|DE|}{|DA|}=sin30° \\
\frac{2}{|DA|}=\frac{1}{2} \\
2=\frac{1}{2}\cdot|DA| \\
|DA|=4$$
b) Obliczenie długości \(|GC|\)
$$\frac{|GC|}{|GD|}=sin30° \\
\frac{|GC|}{2}=\frac{1}{2} \\
|GC|=1$$
c) Obliczenie długości \(|CD|\)
$$\frac{|CD|}{|GD|}=cos30° \\
\frac{|CD|}{2}=\frac{\sqrt{3}}{2} \\
|CD|=\sqrt{3}$$
d) Obliczenie długości \(|BG|\)
$$\frac{|GF|}{|BG|}=cos30° \\
\frac{2}{|BG|}=\frac{\sqrt{3}}{2} \\
2=\frac{\sqrt{3}}{2}\cdot|BG| \\
|BG|=\frac{2}{\frac{\sqrt{3}}{2}} \\
|BG|=\frac{4}{\sqrt{3}}=\frac{4\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{4\sqrt{3}}{3}$$
$$a=|CD|+|DA|=\sqrt{3}+4 \\
h=|BG|+|GC|=\frac{4\sqrt{3}}{3}+1$$
Podstawiając poszczególne długości boków możemy teraz wyliczyć pole naszego trójkąta.
$$P=\frac{1}{2}a\cdot h \\
P=\frac{1}{2}\cdot\left(\sqrt{3}+4\right)\cdot\left(\frac{4\sqrt{3}}{3}+1\right) \\
P=\left(\frac{\sqrt{3}}{2}+2\right)\cdot\left(\frac{4\sqrt{3}}{3}+1\right) \\
P=\frac{4\sqrt{3}\cdot\sqrt{3}}{6}+\frac{\sqrt{3}}{2}+\frac{8\sqrt{3}}{3}+2 \\
P=\frac{12}{6}+\frac{\sqrt{3}}{2}+\frac{8\sqrt{3}}{3}+2 \\
P=2+\frac{3\sqrt{3}}{6}+\frac{16\sqrt{3}}{6}+2 \\
P=4+\frac{19\sqrt{3}}{6}$$
\(P=4+\frac{19\sqrt{3}}{6}\)
błąd w liczeniu odc bg powinno wyjść 4 pierwiastki z 3 prez 3!!!!! przez 30 min się głowiłam nad tym
Odcinek BG jest na pewno dobrze policzony ;) Ale… Twój wynik też jest dobry (po prostu usunęłaś niewymierność z mianownika) :) W sumie to bardzo dobry nawyk z tym usuwaniem niewymierności z mianownika, więc i ja ją usunę w rozwiązaniu :)