Rozwiązanie
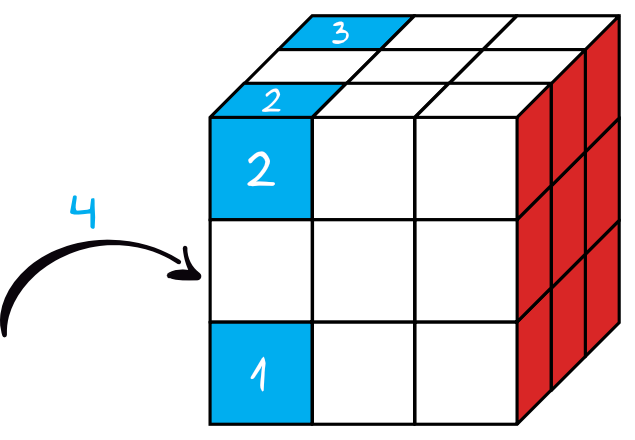
Krok 1. Sporządzenie rysunku pomocniczego.
Sześcian po pomalowaniu i rozcięciu będzie wyglądał mniej więcej w ten sposób:
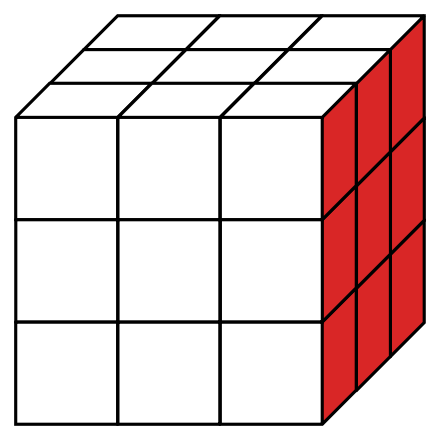
Krok 2. Ocena prawdziwości pierwszego zdania.
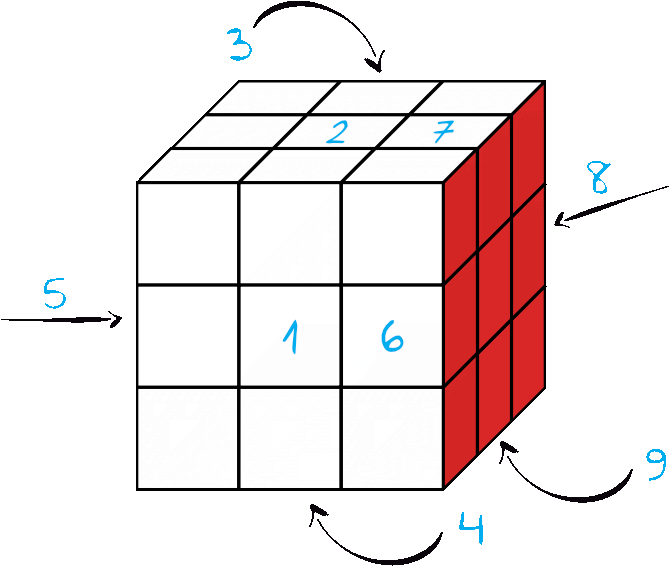
Przyglądając się rysunkowi widzimy, że to zdanie jest nieprawdą. Takich sześcianów jest dokładnie dziewięć. Pięć z nich (ponumerowanych od 1 do 5) to środkowe sześcianiki na każdej ze ścian. Cztery kolejne (z numerami od 6 do 9) to sześciany ze środkowych linii, które stykają się z czerwoną ścianą.
Krok 3. Ocena prawdziwości drugiego zdania.
To zdanie jest prawdą i będą to cztery sześciany znajdujące się w rogach, które nie mają czerwonej ściany: