Rozwiązanie
Krok 1. Zapisanie nierówności.
Aby funkcja liniowa była rosnąca, to współczynnik kierunkowy \(a\) musi być większy od \(0\). W naszym przypadku współczynnik \(a\) jest równy \(m^2-3\), zatem musimy rozwiązać nierówność:
$$m^2-3\gt0$$
Krok 2. Rozwiązanie nierówności.
Naszym zadaniem jest teraz rozwiązanie powstałej nierówności kwadratowej. Tradycyjnie na początku musimy obliczyć miejsca zerowe wielomianu, przyrównując wartość \(m^2-3\) do zera. Możemy to zrobić metodą delty (pamiętając, że w tej sytuacji współczynnik \(b=0\)), ale w tym konkretnym przypadku możemy te miejsca zerowe wyznaczyć znacznie szybciej:
$$m^2-3=0 \\
m^2=3 \\
m=\sqrt{3} \quad\lor\quad m=-\sqrt{3}$$
Mając miejsca zerowe możemy przystąpić do rysowania paraboli. Zaznaczamy na osi wyznaczone przed chwilą miejsca zerowe (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\gt\)) i rysujemy parabolę, która ma ramiona skierowane do góry (bo współczynnik \(a\) jest dodatni).
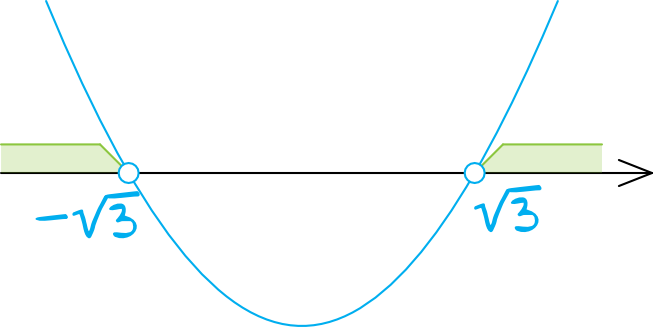
Interesują nas wartości większe od zera, czyli wszystko to, co znalazło się nad osią iksów. Z rysunku jasno wynika, że rozwiązaniem naszej nierówności (a tym samym całego zadania) jest przedział \(m\in(-\infty,-\sqrt{3})\cup(\sqrt{3},\infty)\).