Funkcja liniowa \(f(x)=ax+b\) jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że:
\(a\gt0\) i \(b\gt0\)
\(a\lt0\) i \(b\lt0\)
\(a\lt0\) i \(b\gt0\)
\(a\gt0\) i \(b\lt0\)
Rozwiązanie:
Skoro funkcja liniowa ma być rosnąca, to na pewno \(a\gt0\).
Wiemy też, że funkcja ta ma dodatnie miejsce zerowe, musi więc wyglądać mniej więcej w taki sposób:
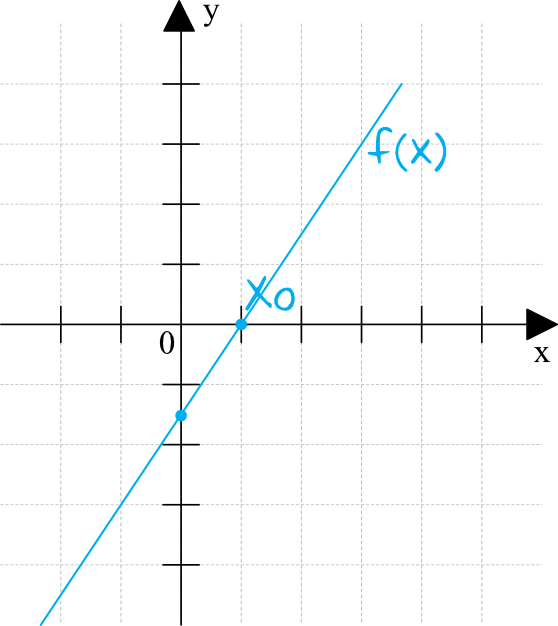
Widzimy wyraźnie, że skoro funkcja ma dodatnie miejsce zerowe i jest jednocześnie rosnąca, to na pewno przecina oś \(Oy\) w wartości ujemnej, czyli pod osią \(Ox\). To oznacza, że współczynnik \(b\lt0\).
Prawidłowa jest zatem odpowiedź \(a\gt0\) i \(b\lt0\).
Odpowiedź:
D. \(a\gt0\) i \(b\lt0\)

