Funkcja kwadratowa jest określona wzorem \(f(x)=(x-1)(x-9)\). Wynika stąd, że funkcja \(f\) jest rosnąca w przedziale:
Wzór funkcji jest podany w postaci iloczynowej, tak więc miejsca zerowe wyznaczymy przyrównując wartość każdego z nawiasów do zera.
$$(x-1)(x-9)=0 \\
x-1=0 \quad\lor\quad x-9=0 \\
x=1 \quad\lor\quad x=9$$
Aby móc określić w jakim przedziale ta funkcja jest rosnąca musimy poznać współrzędną iksową wierzchołka paraboli. I właśnie do uzyskania tej informacji przydadzą nam się miejsca zerowe, które obliczyliśmy w pierwszym kroku, bowiem wierzchołek paraboli będzie pomiędzy po środku między jednym i drugim miejscem zerowym. Zatem:
$$x_{W}=\frac{1+9}{2}=\frac{10}{2}=5$$
Dla przejrzystości zadania zróbmy sobie jeszcze na rysunek szkicowy.
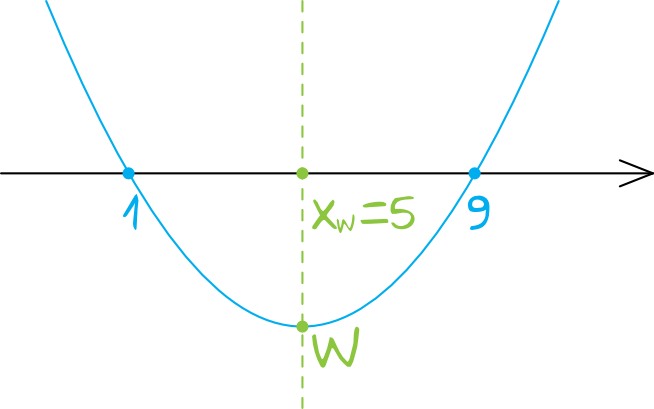
Ramiona paraboli są skierowane do góry, bo przed wartościami \(x\) nie było minusów. Funkcja będzie więc rosnąć od wierzchołka (po to właśnie obliczaliśmy jego współrzędną \(x_{W}\)) aż do nieskończoności. Poszukiwanym przedziałem jest więc \(\langle5;+\infty)\).
A. \(\langle5;+\infty)\)

