Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro funkcja zapisana jest w postaci \(f(x)=x^2+bx+c\), to widzimy, że jej ramiona będą skierowane do góry, gdyż \(a=1\). Z treści zadania wynika, że ta funkcja nie ma miejsc zerowych, zatem w całości musi znajdować się nad osią \(OX\), co prowadzi nas do wniosku, że musi ona wyglądać mniej więcej w ten sposób:
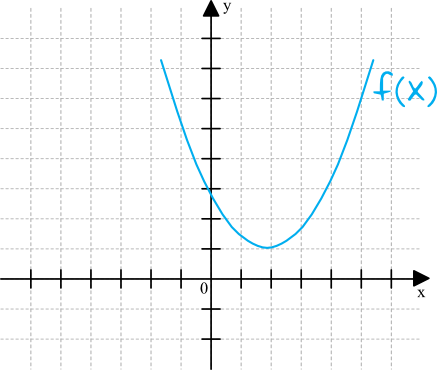
Nie ma dla nas znaczenia, czy ta parabola będzie bardziej po lewej, czy prawej stronie - ważne, że w całości jest nad osią \(OX\).
Warto też zauważyć, że parabola przetnie oś \(OY\) dla dodatniej wartości współrzędnej \(y\). To z kolei oznacza, że na pewno współczynnik \(c\) jest liczbą dodatnią. W tym konkretnym zadaniu z tej własności nie skorzystamy (przynajmniej w zaprezentowanym przeze mnie rozwiązaniu), ale warto o tym pamiętać na przyszłość.
Krok 2. Wykorzystanie informacji na temat miejsc zerowych.
Co się musi stać, aby funkcja kwadratowa nie miała miejsc zerowych? Stanie się tak tylko wtedy, gdy obliczana delta będzie mniejsza od \(0\). Skoro tak, to:
$$b^2-4ac\lt0$$
Wiemy już, że \(a=1\), zatem:
$$b^2-4c\lt0 \\
b^2\lt4c$$
Krok 3. Zakończenie dowodzenia.
Mamy wykazać, że \(1+c\gt b\). Póki co wiemy, że \(4c\) jest większe od \(b^2\). Spróbujmy zatem lekko przekształcić nierówność z treści zadania:
$$1+c\gt b \\
c\gt b-1 \quad\bigg/\cdot4 \\
4c\gt4b-4$$
I tu pojawia się mały problem, bo umiemy wykazać, że \(4c\gt b^2\), a nas proszą o wykazanie, że \(4c\gt4b-4\). Jak to teraz ugryźć? Jeżeli wykażemy, że \(b^2\) jest większe lub równe \(4b-4\), to będziemy pewni, że nierówność z treści zadania jest spełniona. Zapiszmy zatem, że:
$$b^2\ge 4b-4 \\
b^2-4b+4\ge0 \\
(b-2)^2\ge0$$
Jakakolwiek liczba rzeczywista podniesiona do kwadratu jest większa lub równa zero i tak też otrzymaliśmy w powyższej nierówności. To oznacza, że nierówność z treści zadania jest prawdziwa.