Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Jeżeli funkcja kwadratowa ma tylko jedno miejsce zerowe równe \(2\), a w dodatku \(f(0)=8\), to wykres funkcji musi wyglądać mniej więcej w ten oto sposób:
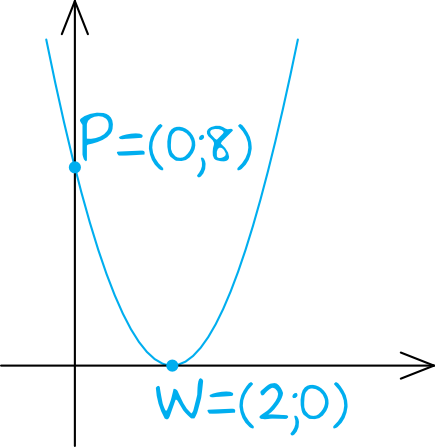
Krok 2. Zapisanie równania w postaci kanonicznej.
Z analizy rysunku wynika, że współrzędne wierzchołka paraboli to \(p=2\) oraz \(q=0\). Znając współrzędne wierzchołka, możemy przystąpić do wyznaczenia wzoru funkcji w postaci kanonicznej, zatem:
$$f(x)=a(x-p)^2+q \\
f(x)=a(x-2)^2+0 \\
f(x)=a(x-2)^2$$
Krok 3. Wyznaczenie współczynnika kierunkowego \(a\) i zapisanie wzoru funkcji.
Do pełnego wzoru brakuje nam tylko znajomości współczynnika kierunkowego \(a\). Aby poznać jego wartość, wystarczy do wyznaczonego wzoru \(f(x)=a(x-2)^2\) podstawić współrzędne jednego z punktów, który należy do wykresu - w naszym przypadku będzie to punkt o współrzędnych \((0;8)\), zatem:
$$8=a(0-2)^2 \\
8=a\cdot(-2)^2 \\
8=4a \\
a=2$$
To oznacza, że wzorem tej funkcji będzie \(f(x)=2\cdot(x-2)^2\) i taka też jest odpowiedź do tego zadania.
Tak na marginesie - nie jest to konieczne, ale możemy też zapisać sobie ten wzór w postaci ogólnej (treść zadania nie precyzuje tego w jakiej postaci ma być podany wzór). W tym celu należy wykonać potęgowanie nawiasu (pamiętając przy okazji o wzorach skróconego mnożenia). Wyglądałoby to w następujący sposób:
$$f(x)=2\cdot(x-2)^2 \\
f(x)=2\cdot(x^2-4x+4) \\
f(x)=2x^2-8x+8$$