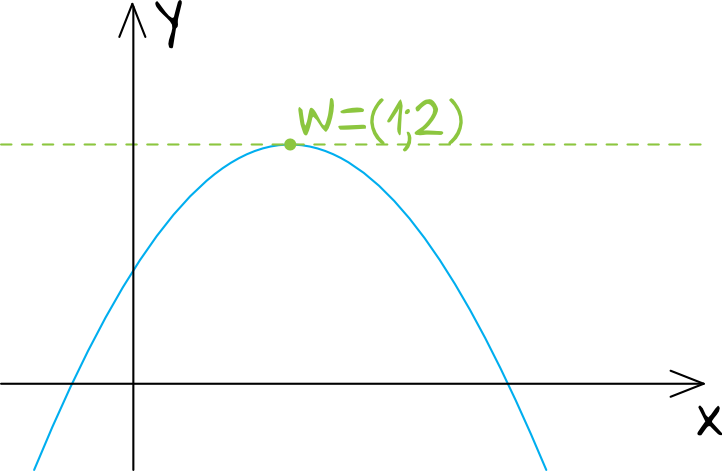
Wyjaśnienie:
Wykres funkcji kwadratowej jest parabolą, a w tym przypadku ta parabola będzie mieć ramiona skierowane do dołu (bo współczynnik \(a=-1\), czyli jest ujemny). To oznacza, że zbiorem wartości będą liczby z przedziału od minus nieskończoności, aż do wartości przyjmowanej w wierzchołku, czyli do \(2\) włącznie. Zbiorem wartości będzie więc przedział \((-\infty,2\rangle\).