Rozwiązanie
Krok 1. Wyznaczenie miejsc zerowych.
Funkcja zapisana jest w postaci iloczynowej, a to oznacza, że bardzo szybko jesteśmy w stanie wyznaczyć jej miejsca zerowe - wystarczy przyrównać wartości w nawiasach do zera:
$$x+2021=0 \quad\lor\quad x-1=0 \\
x=-2021 \quad\lor\quad x=1$$
Krok 2. Sporządzenie rysunku pomocniczego.
Naszkicujmy parabolę, która jest wykresem naszej funkcji, zaznaczając oczywiście wyznaczone przed chwilą miejsca zerowe. Ramiona paraboli będą skierowane do dołu, ponieważ współczynnik \(a\) jest ujemny (\(a=-4\)):
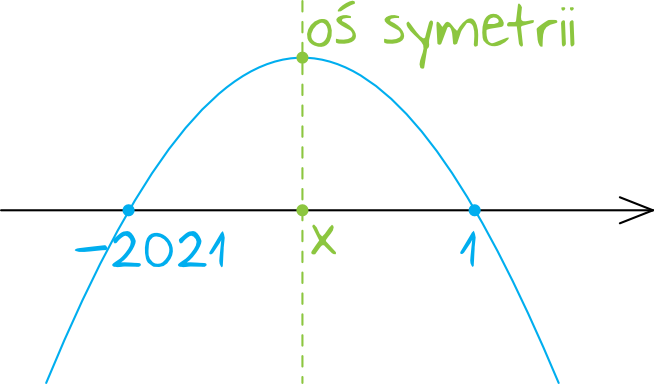
Krok 3. Wyznaczenie osi symetrii wykresu funkcji.
Oś symetrii paraboli ma tę własność, że przechodzi dokładnie między miejscami zerowymi funkcji. Naszą prostą wyznaczymy więc wyliczając średnią arytmetyczną dwóch miejsc zerowych:
$$\frac{-2021+1}{2}=\frac{-2020}{2}=-1010$$
To oznacza, że osią symetrii wykresu tej funkcji jest prosta \(x=-1010\).